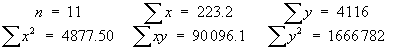ENGI 3423 Probability and Statistics

Faculty of Engineering and Applied Science
2010 Fall

Additional Exercises

[Topics after Test 2]

  1. A production process gives components whose strengths are normally distributed with a mean of 400 N and a standard deviation of 11.5 N.   A modification is made to the process which cannot reduce but may increase the mean strength.   It may also change the variance.   The strengths of nine randomly selected components from the modified process, in Newtons, are: 

     396   402   409   409   414   398   394   436   418

    Test, at a five per cent level of significance, the hypothesis that the mean strength has not increased.

  1. A transport firm is very suspicious of the tyre company’s claim that the average lifetime of its tyres is at least 45,000 kilometres.   The transport company decides to check this claim by fitting forty of these tyres to its trucks, the tyres being a random sample.

    A mean lifetime of 44,164 km with a sample standard deviation of 2,106 km is observed.   What may the transport firm conclude about the claim at a level of significance of one per cent?

  1. A garage wants to know if a more expensive type of radial tyre has a tread life significantly more than 10,000 km beyond the tread life of a cheaper bias-ply tyre.   Only if this is the case will the garage invest in the more expensive type of tyre.   A random sample of forty tyres of each type is tested and the tread lives are measured.   The radial tyres have a mean tread life of 36,500 km with a standard deviation of 2,200 km, while the bias ply tyres have a mean tread life of 23,800 km with a standard deviation of 1,500 km.

    Based on these data, should the garage invest in the radial tyres?

  1. A particular type of motor is known to have an output torque whose range in normal operation follows a normal distribution.   Seven motors are chosen at random and are tested with the old and new methods of controlling the range of torque values.   The results of the tests are as follows:

    Motor: 1234 567
    New method: 5.253.164.436.12 5.752.216.01
    Old method: 7.836.227.468.83 8.195.648.88

    1. Justify your choice of method in (b) below.

    2. Conduct an appropriate hypothesis test to determine whether there is sufficient evidence to conclude that the range of torques with the new method is at least 2 units less than with the old method.

    3. Use the simple linear regression model on these data to find the equation of the line of best fit to these data.

    4. Find the coefficient of determination   R2   and use it to comment on your answer to part (a) above.

  1. A designer claims that a new type of hull increases the average sustained speed of a speedboat by more than 2 km/h over the average sustained speed of the existing hull design.   Random samples of speedboats of the two designs are tested and their sustained speeds (in km/h) are measured on a test course under identical water conditions:

    New design (xA): 
         42    36    38    37    39    36
    Old design (xB): 
     
     30    37    33    31    34

    Conduct an appropriate hypothesis test at a level of significance of 5%.   Is there sufficient evidence to accept the designer’s claim?   What assumptions have you made?

  1. The true mean tensile strength of a new type of lightweight cable is claimed to be more than 20 kN.   The distribution of actual strengths is known to be normal to a good approximation, with a standard deviation of 1.4 kN.   A random sample of five of the new cables has a mean of 21.5 kN

    1. Is there sufficient evidence to support the claim?

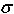    2. Now suppose that the standard deviation   sigma   is unknown and that the measured standard deviation of the random sample is s = 1.4 kN.   Is there sufficient evidence to support the claim?

  1. Random samples are drawn from two independent populations, producing the following summary statistics:

    nX = 50 xBar = 643 sX = 26 nY = 90 yBar = 651 sY = 32

    Are these data consistent with the hypothesis that the two population means are equal?

  1. A study of company performance in two nearby cities was conducted to test for any significant difference between the companies in those cities.   A random sample of ten companies in city A had a sample mean performance index of 74.3 with a standard deviation of 3.2 .   A random sample of ten companies in city B had a sample mean performance index of 73.2 with a standard deviation of 2.9 .

    Is there a significant difference in company performance index between these two cities?   State carefully your assumptions and your hypotheses.

  1. A study was conducted to analyze the relationship between advertising expenditure and sales.   The following data were recorded:

    X Y
      Advertising ($)     Sales ($)  
    20 310
    24 340
    30 400
    32 420
    35 490

    Assume a simple linear regression between sales Y and advertising X.   Calculate the coefficients β0 and β1 of the line of best fit to these data and estimate the sales when $28 are spent on advertising.

    Is there a significant linear association between Y and X?

  1. [Devore 6th ed., Ch. 12 p. 551 q. 73 - parts (b) & (c) are bonus questions only]

    The accompanying set of data is a subset of the data that appeared in the paper “Radial Tension Strength of Pipe and Other Curved Flexural Members” (J. Amer. Concrete Inst., 1980, pp. 33-39).   The variables are age of a pipe specimen (x in days) and load necessary to obtain a first crack (y in 1000 lb/ft).

    x 20 20 20 25 25 25 31 31 31
    y 11.45 10.42 11.14 10.84 11.17 10.54 9.47 9.199.54

    1. Calculate the equation of the estimated regression line.
    2. *   Suppose that a theoretical model suggests that the expected decrease in load associated with a 1 day increase in age is at most .10 (× 1000 lb/ft).   Do the data contradict this assertion?   State and test the appropriate hypotheses at significance level .05 .
    3. *   For purposes of estimating the slope of the true regression line as accurately as possible, would it have been preferable to make a single observation at each of the ages 20, 21, 22, ..., 30 and 31?   Explain.
    4. Calculate an estimate of true average load to first crack when age is 28 days.   Your estimate should convey information regarding precision of estimation.

  1. [Bonus question, to provide practice in the supplementary topic of type II error probabilities.]

    Find the probability of committing a type II error when the true population mean is µ = 104 and an upper-tail hypothesis test is conducted at a level of significance of five per cent with a random sample of size 25 on the null hypothesis that µ = 100.   It is known that the population variance is 100.

    Repeat your calculation in the case when the level of significance of the hypothesis test is one per cent.

  1. [Bonus question, to provide practice in the supplementary topic of type II error probabilities.
    This question is a modification of Devore, 6th ed., Ch. 8.3, pp. 343-344, q. 38.]

    A university library ordinarily has a complete shelf inventory done once every year.   Because of new shelving rules instituted the previous year, the head librarian believes it may be possible to save money by postponing the inventory.   The librarian decides to select 800 books at random from the library’s collection and to have them searched in a preliminary manner.   If the evidence indicates strongly that the true proportion of misshelved or unlocatable books is less than .02, then the inventory will be postponed.

    1. Among the 800 books searched, 12 were misshelved or unlocatable.   Test the relevant hypotheses (at a level of significance of .05) and advise the librarian what to do.

    2. If the true proportion of misshelved and lost books is actually .01, what is the probability that the inventory will be [unnecessarily] taken?

    3. If the true proportion is .05, what is the probability that the inventory will be postponed?

    4. What types of errors are the events described in parts (b) and (c) above?

  1. [Bonus question only]     [Devore 6th ed., Ch. 9.4 p. 398 q. 55]

    Two different types of alloy, A and B, have been used to manufacture experimental specimens of a small tension link to be used in a certain engineering application.   The ultimate strength (in ksi) of each specimen was determined and the results are summarized in the frequency distribution tabulated below.

    Alloy: A B
    26 - under 30 6 4
    30 - under 34 12 9
    34 - under 38 15 19
    38 - under 42 7 10
    sample sizes 40 42

    1. Compute a 95% confidence interval for the difference between the true proportions of all specimens of alloys A and B that have an ultimate strength of at least 34 ksi.

    2. Can you conclude that there is a significant difference between these two population proportions?

  1. [Devore, ex. 12.4, q. 50 modified]

    An experiment to measure the macroscopic magnetic relaxation time in crystals (in microseconds, µs) as a function of the strength of the external biasing magnetic field (in kiloGauss, kG) yielded the following data (“An Optical Faraday Rotation Technique for the Determination of Magnetic Relaxation Times”, IEEE Trans. Magnetics, June 1968: 175-178, with data read from a graph that appeared in the article).

    x 11.012.515.2 17.219.020.8 22.024.225.327.029.0
    y 187225305318367365 400435450506558

    The summary statistics are:
            n = 11 , sum x = 223.2 , sum y = 4116 sum x^2 = 4877.50 , sum xy = 90,096.1 , sum y^2 = 1,666,782

    1. Fit the simple linear regression model to these data.
    2. What proportion of the total variation in Y is explained by the linear regression model?
    3. Calculate a 95% confidence interval for the expected relaxation time when the field strength is 18 kG.
    4. Calculate a 95% prediction interval for a future relaxation time when the field strength is 18 kG.

  Return to Index of Problem Sets   [Return to the Index of Problem Sets.]   [Solutions to this problem set] To the solutions to this problem set
  Back to previous page   [Return to your previous page]
Created 1997 11 27 and most recently modified 2010 07 30 by Dr. G.H. George.