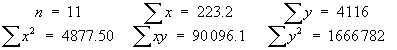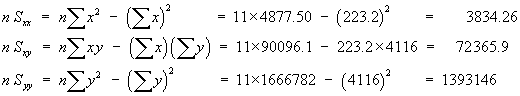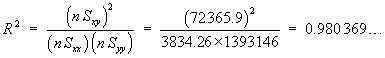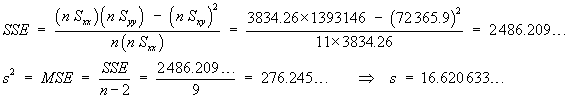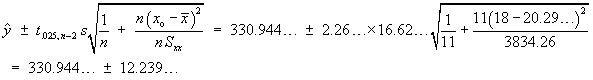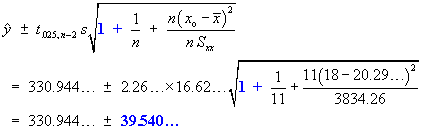A production process gives components whose strengths are normally distributed with a mean of 400 N and a standard deviation of 11.5 N. A modification is made to the process which cannot reduce but may increase the mean strength. It may also change the variance. The strengths of nine randomly selected components from the modified process, in Newtons, are:
396 402 409 409 414 398 394 436 418 |
Test, at a five per cent level of significance, the hypothesis that the mean strength has not increased.
Let X = component strength (N)
X ~ N(µ,
σ2)
Test
![]() :
µ = 400
vs.
:
µ = 400
vs.
![]() :
µ > 400
at α = .05
:
µ > 400
at α = .05
σ2 is unknown for the
new process.
|
Data: |
n = 9 | åx = 3676 | åx2= 1502838 | a = 0.05 |
|
|
|
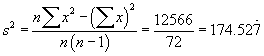 |
s = 13.21089617 | |
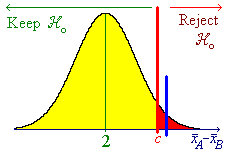
Method 1
![[Graph showing rejection region]](aximages/sxq1.gif) |
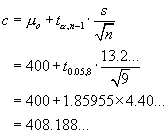 |
![]()
\
Reject
![]() in favour of
in favour of
![]() at a = 0.05
at a = 0.05
OR
Method 2
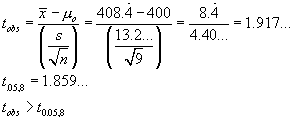
\
Reject
![]() .
.
OR
Method 3
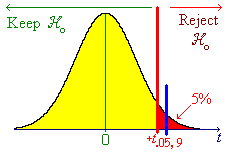
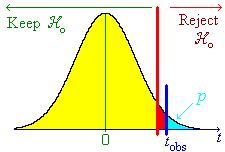
From t-tables, t.05, 8 = 1.859...
and t.025,8 = 2.306...
.025 < P[T>tobs] < .05
and
a = .05
[From appropriate software,
P[T>tobs] = .045 <
a]
\
Reject
![]() .
.
OR
Confidence Interval Method
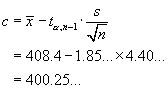
\ we are “95% sure that
µ > 400.25...”.
µ = 400 is not inside this CI.
\
Reject
![]() .
.
At a = 5%, there is sufficient evidence
to conclude that
| there has been an increase in mean strength. |
|---|
An Excel spreadsheet file and a Minitab project file are also available to illustrate this solution.
![[Graph showing rejection region]](aximages/sxq2.gif)
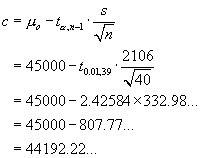
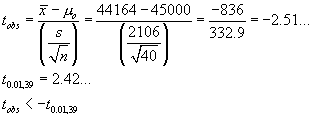
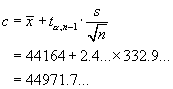
![[Graph of rejection region]](aximages/sxq3.gif)
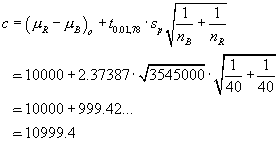
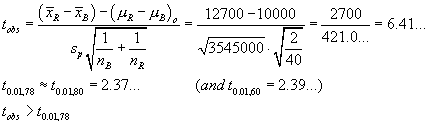
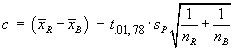
![[Graph of rejection region]](aximages/sxq4.gif)
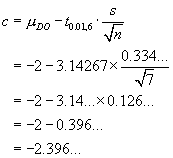
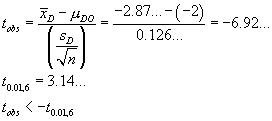
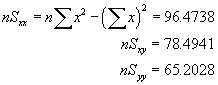
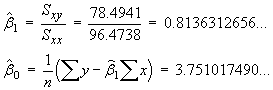
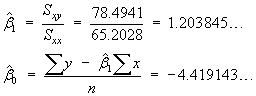
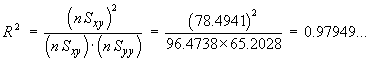
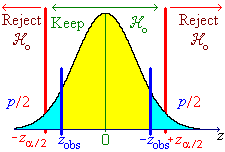
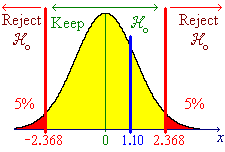
![V[XbarA-XbarB] = sA^2/nA - sB^2/nB](aximages/q5vx2.gif)
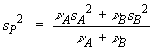
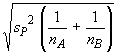 =
=
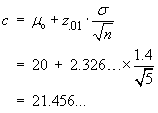
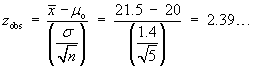
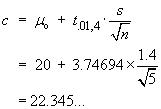
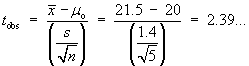
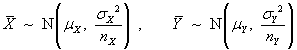
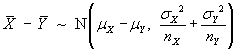
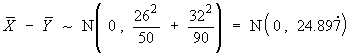
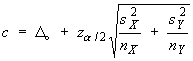
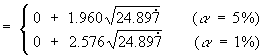
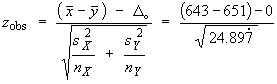
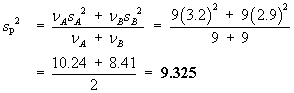
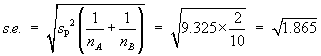
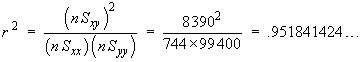
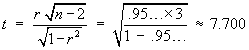
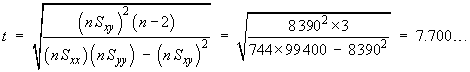
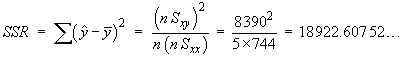
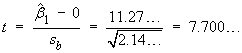
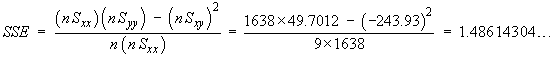
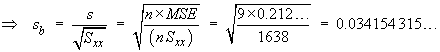
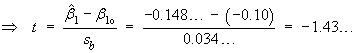
![t = {(nSxy) - beta1o*(nSxx)} *
sqrt{(n-2) / [(nSxx)(nSyy) - (nSxy)^2]} = -1.43...](aximages/q10bt2.gif)
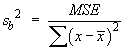 .
A smaller value of sb leads
to more precise estimates of the slope.
.
A smaller value of sb leads
to more precise estimates of the slope.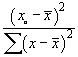 .
These intervals are narrower when the denominator
.
These intervals are narrower when the denominator
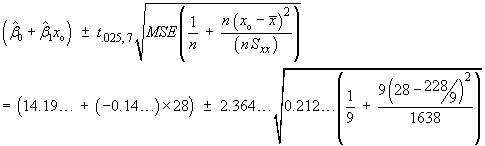
![= P[Z < (c-104) / s.e.]
= Phi((103.290 - 104) / 2)](aximages/q11aprob2.gif)
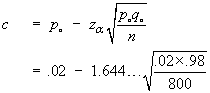
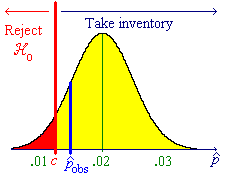
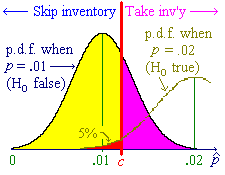
![P[P^ < c] = Phi((c-.01)/sqrt{.01x.99/800})
= Phi(.001857.../.003517...) = Phi(0.52807)](aximages/q12bprob2.gif)
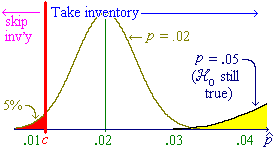
![P[P^ < c] = Phi((c-.05)/sqrt{.05x.95/800})
= Phi(-.038142.../.007705...) = Phi(-4.95) = 0](aximages/q12cprob2.gif)