ENGI 3423 Probability and Statistics

Faculty of Engineering and Applied Science
2010 Fall

Practice Questions

for Term Test 1
[Descriptive Statistics and Elementary Probability]

Compare your solution with the files listed on the solution page.

  1. Note that this question attempts to cover various aspects of descriptive statistics.   In the actual test, there will be time to test only a portion of what is presented here.   Only some of the information shown here will be presented in a question on the test.

    The actual time, in hours, to failure of a prototype mechanical component in a turbine, is measured on fifty occasions in an experiment.   The raw results are displayed here, sorted into increasing order:

    11 14 20 23 31 36 39 44 47 50
    59 61 65 67 68 71 74 76 78 79
    81 84 85 89 91 93 96 99101104
    105105112118123 136139141148158
    161168184206248 263289322388513

    The summary statistics include
              n = 50, Sum(x) = 5963 , Sum(x^2) = 1176795

    1. From the summary statistics, calculate the sample mean and sample standard deviation for these data.
    2. From the histogram below, identify the modal class.
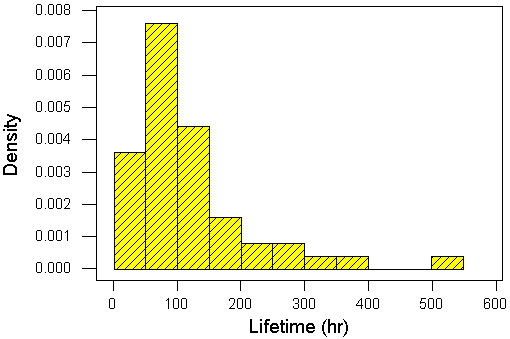
      histogram of lifetime data
    3. What evidence is there, from the histogram, for skewness?
    4. Use the histogram only, to estimate the number of components in the sample, whose lifetimes are less than 50 hours.
    5. A stem-and-leaf diagram for these data is
          9    0 112233344
  (19)   0 5566667777788889999
   22    1 00001123344
   11    1 5668
    7    2 04
    5    2 68
    3    3 2
    2    3 8
    1    4 
    1    4 
    1    5 1
      Use this stem-and-leaf diagram to construct a frequency (and cumulative frequency) table and hence find the median class.
    6. Find the median value from the original data.
    7. The asterisk in the boxplot below denotes the location of the sample mean.
      Describe the evidence for skewness that you can see in the boxplot.
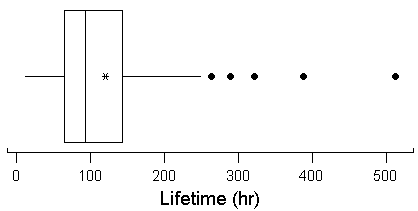
      boxplot of lifetime data
    8. List all the outliers.

  1. A box contains 11 different [distinguishable] gear wheels.   In how many ways can 3 gear wheels be drawn from the box, if they are drawn

    1. with replacement (order of selection matters)?
    2. without replacement (order of selection matters)?
    3. without replacement (order of selection is irrelevant)?
    Show your calculations in each case.

  1. Each of 12 refrigerators of a certain type has been returned to a distributor because of the presence of a high-pitched oscillating noise when the refrigerator is running.   Suppose that four of these 12 have defective compressors and the other eight have less serious problems.   If they are examined in random order, let X = the number among the first six examined that have a defective compressor.   Compute

    1. P[ X = 1]
    2. P[ X > 4]
    3. P[1 < X < 3]

  1. [from Devore]
    A mathematics professor teaches both morning and afternoon sections of a course.
    Let A = {the professor gives a bad morning lecture}
    and B = {the professor gives a bad afternoon lecture}.
    If P[A] = .3 ,   P[B] = .2   and P[A Ù B] = .1 ,   then calculate the following probabilities (a Venn diagram might help) and calculate the equivalent odds:

    1.   P[B | A]
    2.   P[~B | A]
    3.   P[B | ~A]
    4.   P[~B | ~A]

    5. If, at the conclusion of the afternoon class, the professor is heard to mutter “what a rotten lecture”, then what is the probability that the morning lecture was also bad?

    1. An engineer states that the odds of a prototype microchip surviving a current of 3 µA for 2 hours is “4 to 1 against”.   What is the engineer’s probability for this event?

    2. The event E is defined to be
            “the score on a roll of a fair die is either a prime number or 1”.
      Calculate the odds on E, expressed as a ratio reduced to its lowest terms.

  1. Odds vs. Bookies’ Odds

    In a five horse race, you can place a bet of $180pi and if event   Ei (= horse i wins) occurs, then you win the bookie’s stake of $180.   The stake is the same for every horse.
    The bookie quotes odds of

    r1 = 5 to 4 on, r2 = 3 to 1 against, r3 = 7 to 2 against,
    r4 = 17 to 1 against

    and r5 = 17 to 1 against

    1. Are these odds fair?   Justify your answer by determining whether or not the probabilities associated with these odds are coherent.
    2. What is the bookie’s guaranteed profit if you place one bet on each of all five horses?

  1. An electronic [or structural] system consists of five electronic [or structural] components arranged as follows:
    Circuit A to R1 to [parallel: (series {parallel R2, R4}, R5), R3] to B

    Each component is operative or fails under load.   The probability of failure for each individual component is .01.   The entire assembly fails only if the path from A to B is broken.   The sample space S consists of all possible arrangements of operative and inoperative components.

    1. Show that n(S) = 32.

    Let E1 = "the assembly is operative";
          E2 = "R2 has failed but the assembly is operative";
          E3 = "R3 has failed but the assembly is operative";
    and F = "the assembly has failed".

    1. Are E1 and E2 mutually exclusive?
    2. Are E1 and E3 mutually exclusive?
    3. Are E2 and E3 mutually exclusive?
    4. Write down all the sample points in the event F, (that is, list all arrangements of operative and inoperative components that lead to the failure of the entire assembly).   Hence find n(F).
    5. Are the sample points in the event F equally likely?
    6. What is the probability that the assembly fails?
      [You may assume that component failures are independent of each other]

  1. There are seven candidates in an election for three officers on the executive committee of a club.   In how many distinct ways can the voting members of the club fill the three vacancies if

    1. the three officer positions are identical (for example, they are all committee members without specific office);
    2. the three officer positions are distinct (for example, the person with the most votes becomes president and the runner-up becomes vice president);

  1. A certain rare disease is known to occur in 1% of the population.
    A diagnostic test exists for this disease, but the test is not perfect.
    If a person has the disease, then the test will [correctly] detect the disease 98% of the time.
    If a person does not have the disease, then the test will [incorrectly] claim a detection of the disease 10% of the time.

    Given a positive test result [implying that the person has the disease], what are the odds that the test result is correct, [the person really does have the disease]?

  1. Adam Ant is determined to return to his home I from his Aunt’s house A over the lattice of twigs shown below. 

               A ---- B ---- C
           |      |      |
           |      |      |
           D ---- E ---- F
           |      |      |
           |      |      |
           G ---- H ---- I

    Being only a young ant, he can only move south (down the page) or east (right) at each junction.   Where there is a choice, Adam is equally likely to choose each of the two twigs.

    1. Write down the complete list of outcomes.
      (For example, one of the possible outcomes is the path ABEFI).
    2. Let X represent the number of junctions along the path at which Adam has a choice of twig.   Write down the complete set of possible values of X.
    3. For each possible value of X, find the probability that that value of X occurs.
      [Be careful:   P[X = 2] is not 1/3 !]

Also see the Term Tests from the years 2008, 2007 and 2006.

  Return to Index of Problem Sets   [Return to the Index of Problem Sets.]   [Solutions to these questions] To the solutions to these questions
  Back to previous page   [Return to your previous page]
Created 1999 07 30 and most recently modified 2010 07 30 by Dr. G.H. George