ENGI 4421 - Third Minitab Tutorial
Normal Probability Plot & Confidence Interval
Simulations using MINITAB

•   create a simulated set of data for use in Minitab,
•   display a graphical summary of the data,
•   produce a normal probability plot for the data,
•   construct a one-sample confidence interval on the mean,
•   use Excel^® to produce a normal probability plot for the data.

Creation of a Data Set

We shall simulate the creation of a normal probability plot for a case non-normal, namely data drawn from an exponential distribution. The standard exponential distribution (λ = 1) is shown here: We shall reproduce the lamp life time simulation from tutorial #2. Start Minitab. Click on the menu item "Calc" Move to "Random Data" On the new pop-up menu, click on "Exponential..."

---

In the new dialog box, Enter 100 for the number of rows, Type C1 for the location ('Store in column(s)' pane), Enter 1000 for the Scale, Leave the Threshold at 0 and Click on the "OK" button.

---

Type a new name for column C1 . As lifetimes are often random quantities that follow an exponential distribution, we shall use the name Lifetime here. The column Lifetime now contains 100 values. Note that this is a set of random data. The numbers in your data column will not be identical to those shown here.

Graphical Summary of the Data

As we have done before, we can use Minitab to gain a first impression of the distribution of our newly-generated data. Click on the menu item "Stat", Move to "Basic Statistics" and Click on "Display Descriptive Statistics...".

---

In the left pane of the dialog box, double click on "C1 Lifetime" to select it into the "Variables" pane, then click on the "Graphs..." button.

---

In the new dialog box, Check the boxes "Histogram of data, with normal curve" and "Boxplot of data" and Click on the "OK" button. Back in the "Display Descriptive Statistics" window, click on the "OK" button.

---

Two graphs then appear in the output pane:

The evidence for positive skew is overwhelming.
The histogram shows a long right tail and no left tail.


The boxplot shows the upper quartile to be further away from the median than the lower quartile.
The boxplot’s upper whisker is much longer than its lower whisker.
There are several outliers, all on the positive side.

From the top of the output pane,

The mean is much greater than the median.

[Note also that the values of sample mean and sample standard deviation are consistent with equality of the population mean and population standard deviation, which is true of any exponential distribution.]

Clearly the normal distribution does not fit these data.

Normal Probability Plot — Minitab

Click on the menu item "Graph", then Click on "Probability Plot..."

---

Accept the default "Single" Just click on the "OK" button.

---

In the left pane of the dialog box,

Double click on "C1 Lifetime" to select it into the "Graph variables" pane, then



Click on the "Labels..." button.

---

Provide a more meaningful title for the normal probability plot.



Then click on the "OK" button.
Back in the "Probability Plot" window, click on the "OK" button.

---

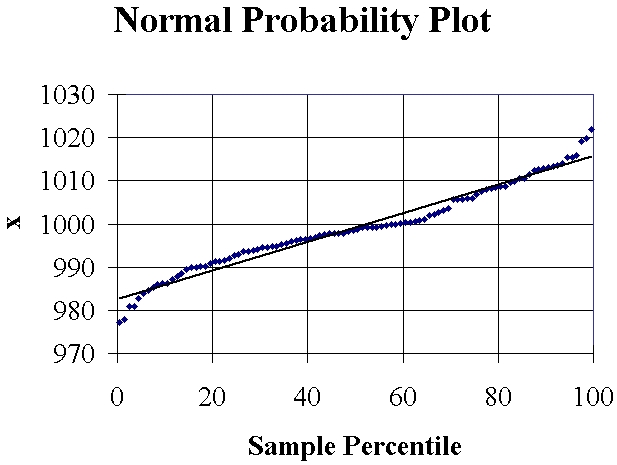
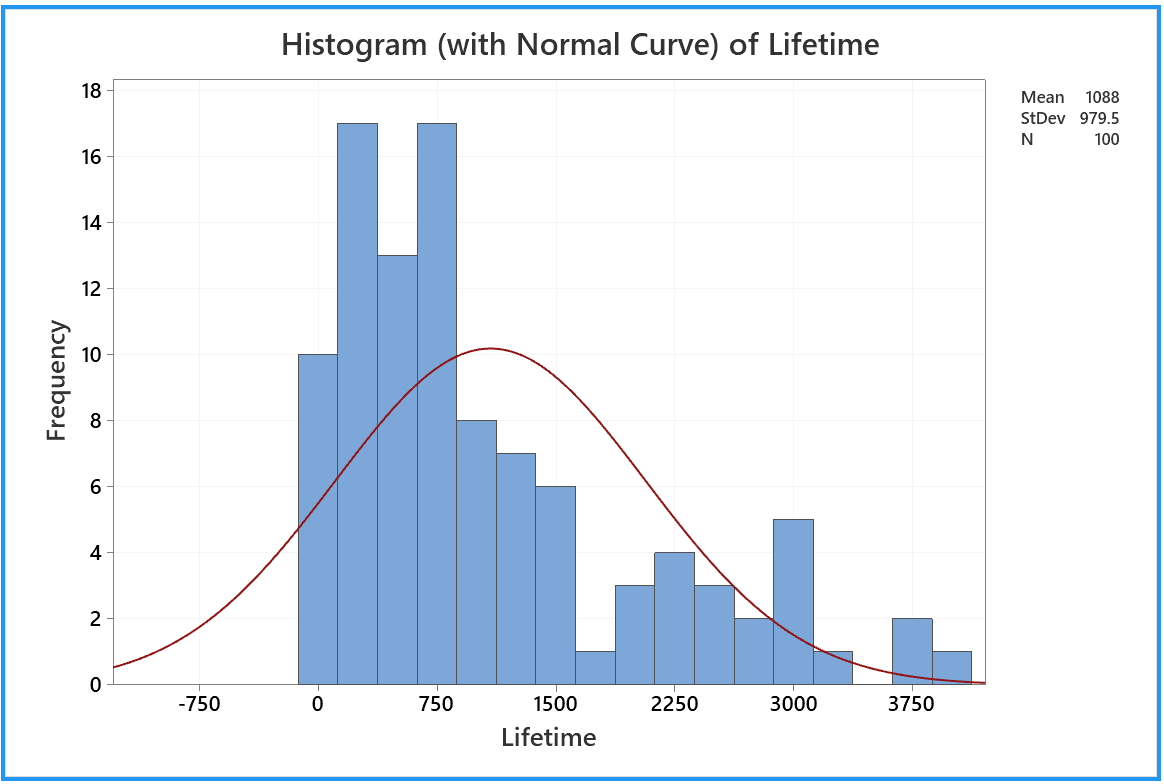
The following normal probability plot (or something very like it) then appears in a new tab of the output pane:



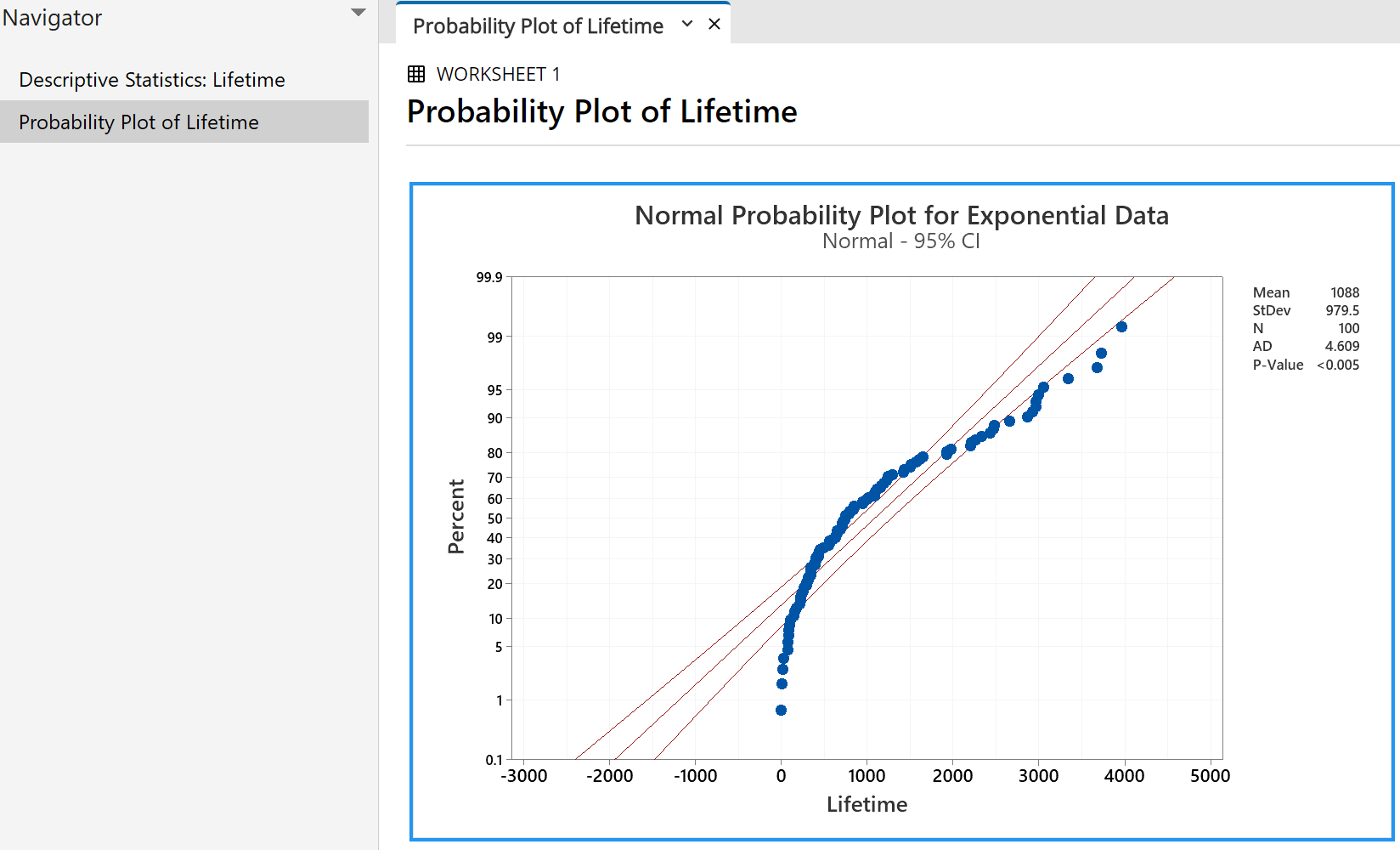
A random sample of size 100, drawn from a normal distribution, will have all (or nearly all) of its points near the straight line of a normal probability plot.   Only 5% of all points will fall, by chance, outside the two curves on either side of the line.
Clearly this data set has not been drawn from a normal distribution.

---

Here are some other normal probability plots (as produced by Version 19 of Minitab - similar to Versions 13 to 18).

The set-up is similar to the steps above, except for drawing the samples from other probability distributions.

In the worksheet in the data pane, name column 2 as 'Normal'.

---

For a sample drawn from the standard normal distribution: Click on the menu item "Calc" Move to "Random Data" On the new pop-up menu, click on "Normal..."

---

Enter 100 as the 'Number of rows of data to generate'. Click in the right pane 'Store in column(s)'. Choices appear in the left pane. In the left pane of the dialog box, double click on 'C2 Normal'. Leave the 'Mean' and 'Standard deviation' at their default values. Click 'OK'.

---

Click on the menu item "Graph", then Click on "Probability Plot..."

---

As before, accept the default "Single" Just click on the "OK" button.

---

Minitab remembers your choices from your previous visit to this dialog box in this session. In the left pane, double click on 'C2 Normal' to replace the graph variable. Then click on the 'Labels' button.

---

Again Minitab remembers your most recent choice. Replace the word 'Exponential' by the word 'Normal'. Then click 'OK' on this and the previous dialog boxes.

---

A new tab appears in the output pane.

100 data drawn from a standard Normal distribution   N(0, 1)



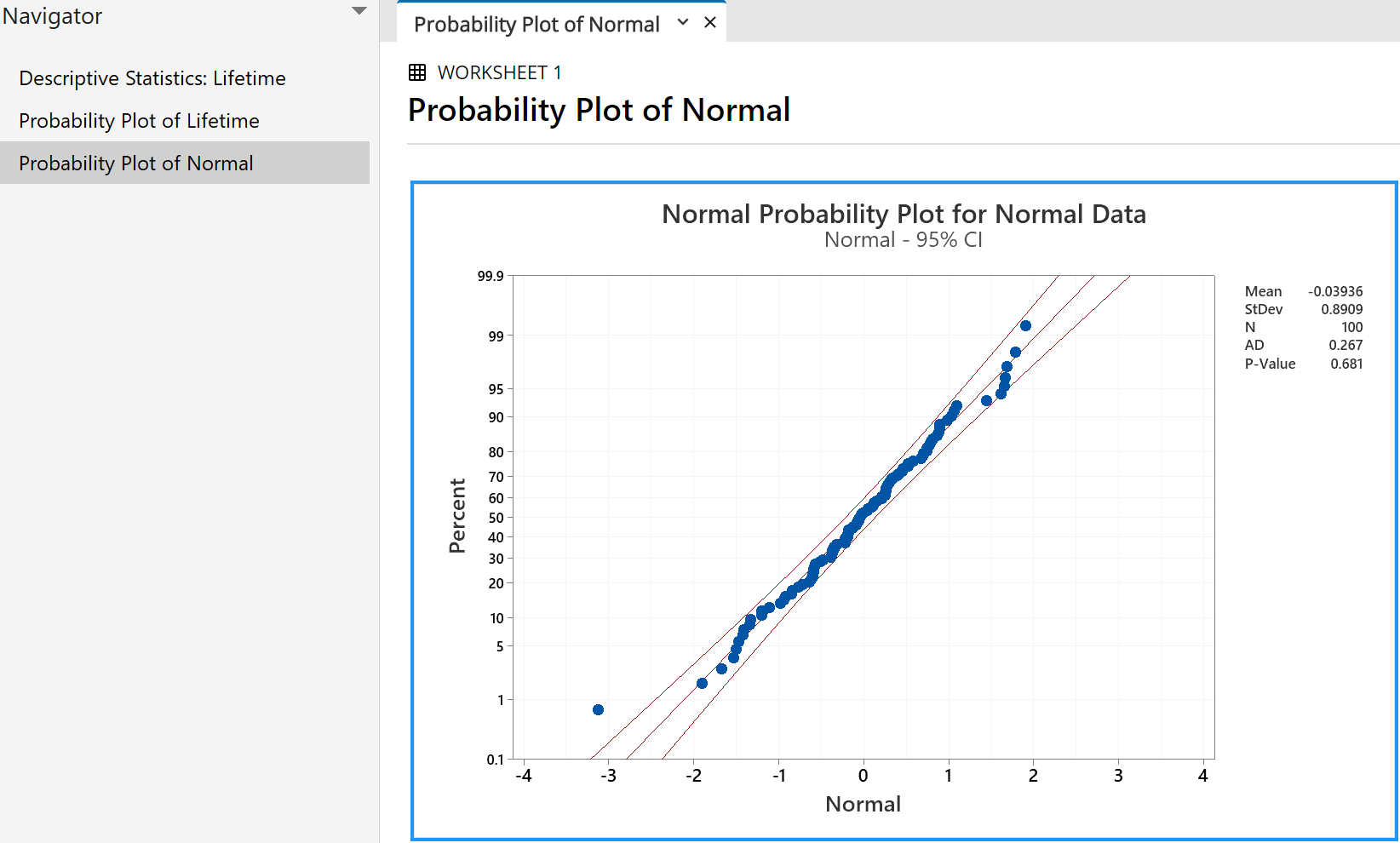
Note how nearly all points lie within the two curves, close to a straight line.
In this simulation, only one of the 100 points is clearly outside the 95% confidence bands.
The 'P-value' of 0.681 indicates that 68.1% of all future samples drawn randomly from this population will show a greater deviation from the ideal normal distribution than this sample does.   We are therefore very confident that this sample came from the standard normal distribution (which, of course, it did!).

---

Similar steps allow us to explore normal probability plots for samples drawn at random from other probability distributions.

100 data drawn from a standard LogNormal distribution.



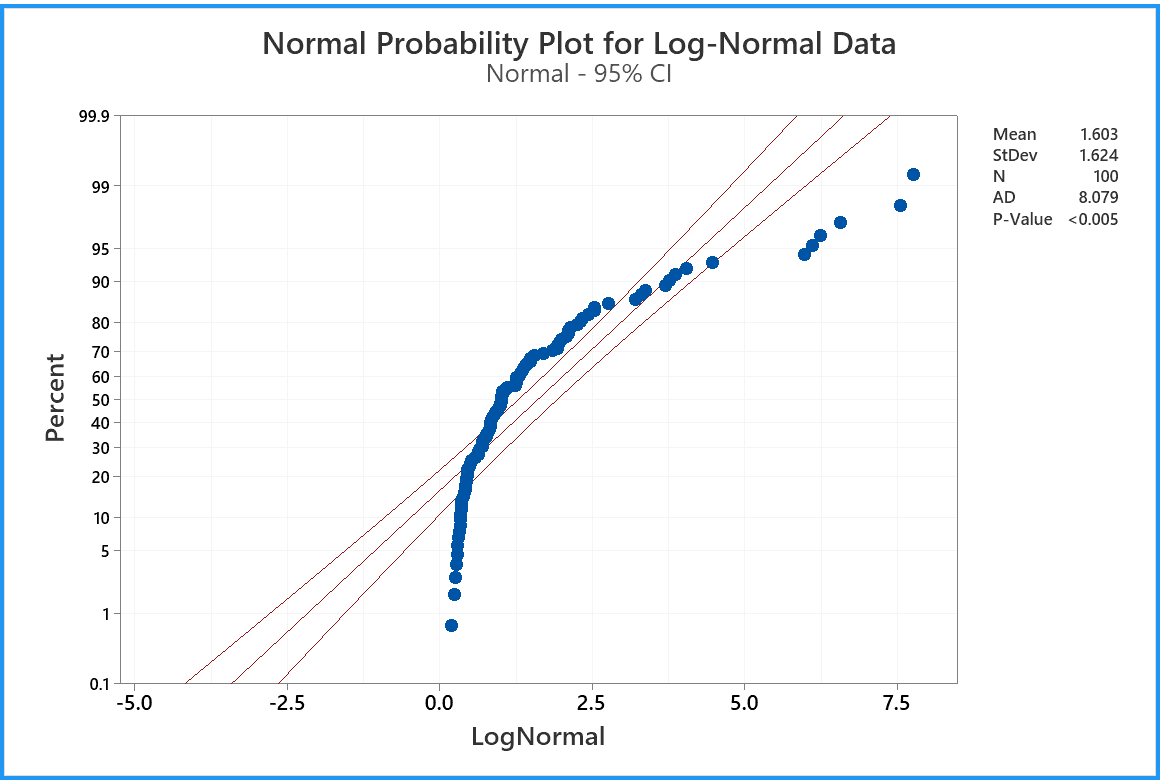
Note how this plot resembles that for the exponential distribution.

---

100 data drawn from a Cauchy distribution of mean 0 and semi-interquartile range 1.



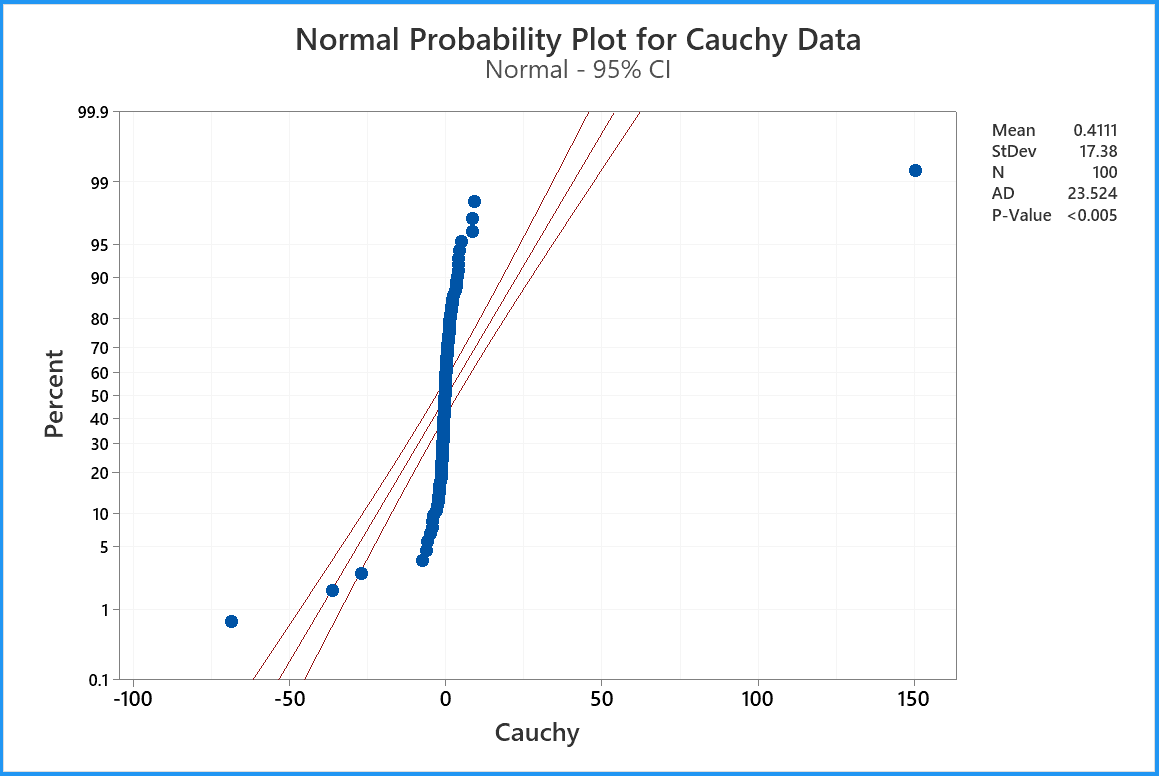
This plot reveals the very heavy tails of the Cauchy distribution.
For the run that produced this plot, the 100 data values had a sample median very close to the population median value of zero and quartiles near ±1 (which usually happens).   By chance, very extreme outliers on both sides (dozens of interquartile ranges away from the median) cancelled out to leave this sample mean close to zero.   If you draw more random samples from the same Cauchy distribution, you will find instances when the sample mean is far away from the population mean of zero.

Recall from the last question of Problem Set 5 that the Cauchy distribution has a finite interquartile range but an infinite population variance, which renders the sample mean completely unstable.

---

100 data drawn from a Beta distribution Beta(18, 2).



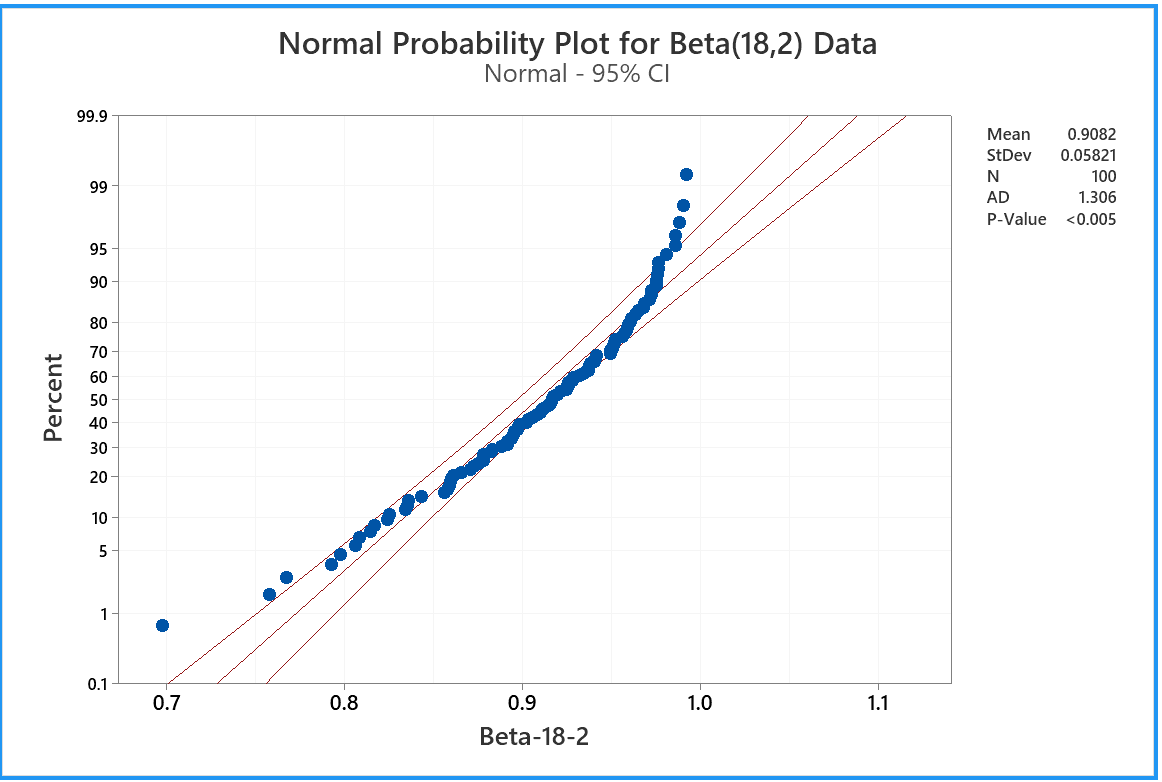
Note how this plot reveals a strong negative skew, together with the light right tail.   The plot clearly shows that these data are inconsistent with a normal distribution.

---

Here is one example of a non-normal probability plot.

As before, click on 'Graph' then 'Probability Plot...', then 'Single' and 'OK'.

In the 'Probability Plot: Single' dialog box,

click on the 'Distribution' button.

---

In the 'Probability Plot: Distribution' dialog box, first tab 'Distribution',
pull down the menu for 'Distribution' and click on 'Exponential'

Then click 'OK'.   You should also adjust the label.

---


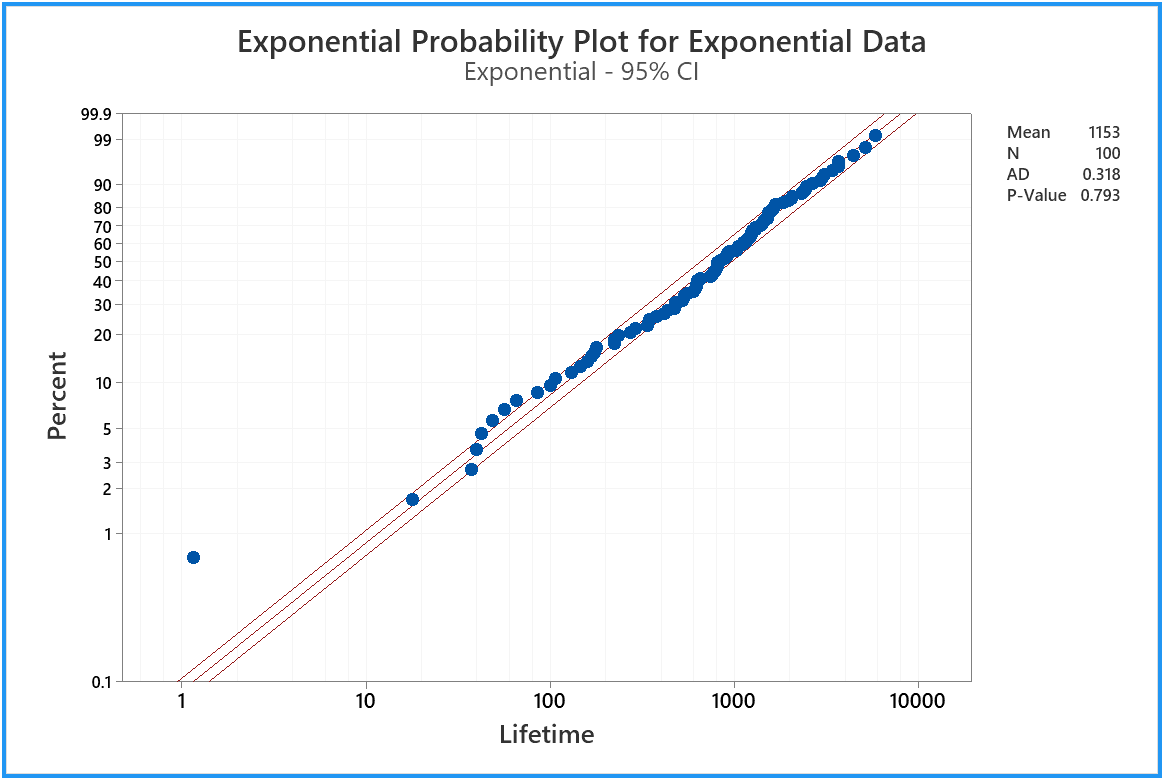
Now we can see that our 'Lifetime' sample is consistent with having been drawn from an exponential distribution (which, of course, it was!)

---

Feel free to explore other features of Minitab’s powerful probability plot options, such as changing the confidence intervals from 95% to 99%, or changing the normal probability plot to a probability plot for another distribution.

You can export the results from the various tabs of the output pane to Word.
Then save your work and exit from Minitab.

---

The populations from which these data sets came are illustrated here, in their standard forms.


standard exponential	standard normal
standard log-normal	standard Cauchy
beta (18, 2)

Normal Probability Plot — Excel

Open Excel and import the data set, for which you wish to create a normal probability plot, into a column.

Check that the Analysis Tool Pack is present, as follows. Click on the menu item "Tools" and check if the item "Data Analysis..." is present in that drop down list. If it is present, then bypass the next step. Otherwise, click on "Add-Ins...".

---

Check the options for "Analysis ToolPak" and "Analysis ToolPak - VBA" then click on the "OK" button.

---

Alongside the genuine data, place a column containing the same number of values. The new values can be any set of distinct numbers. They are needed for the next two steps.

---

Click on the menu item "Tools" and then Click on "Data Analysis...".

---

Scroll down the list of Analysis Tools and click on "Regression" then click on the "OK" button.

---

In the Regression dialog box: Select the range where your data are stored as the "Input Y Range". Select the range where the junk data are stored as the "Input X Range". Choose a location for the tables of values, (most of which will be irrelevant!).   In this example, a separate tab has been chosen. Check the last box "Normal Probability Plots" and leave all other boxes unchecked. then click on the "OK" button.

---

At the location where the output was chosen to be, various tables and a graph appear.



---

Resize the graph and move it to another tab.
Right-click on any of the plotted points.



Click on "Add Trendline...".
In the new dialog box, accept the default option (linear trend) and
click on the "OK" button.
You may also wish to tidy the graph up somewhat, to produce a result like this:


The Excel file is available here.

Clearly Minitab does a far superior job of constructing probability plots than Excel can!

Confidence Intervals

We shall use Minitab to

• simulate drawing a random sample from a known normal population,
• construct one- and two-sided confidence intervals for the mean,
• draw inferences on the true value of the mean from the confidence intervals.

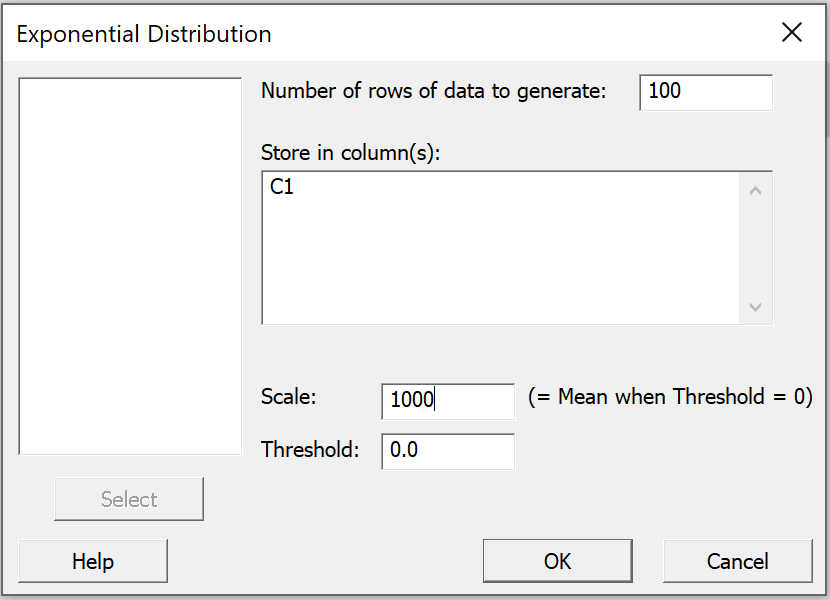
In a new project, begin by naming column C1

---

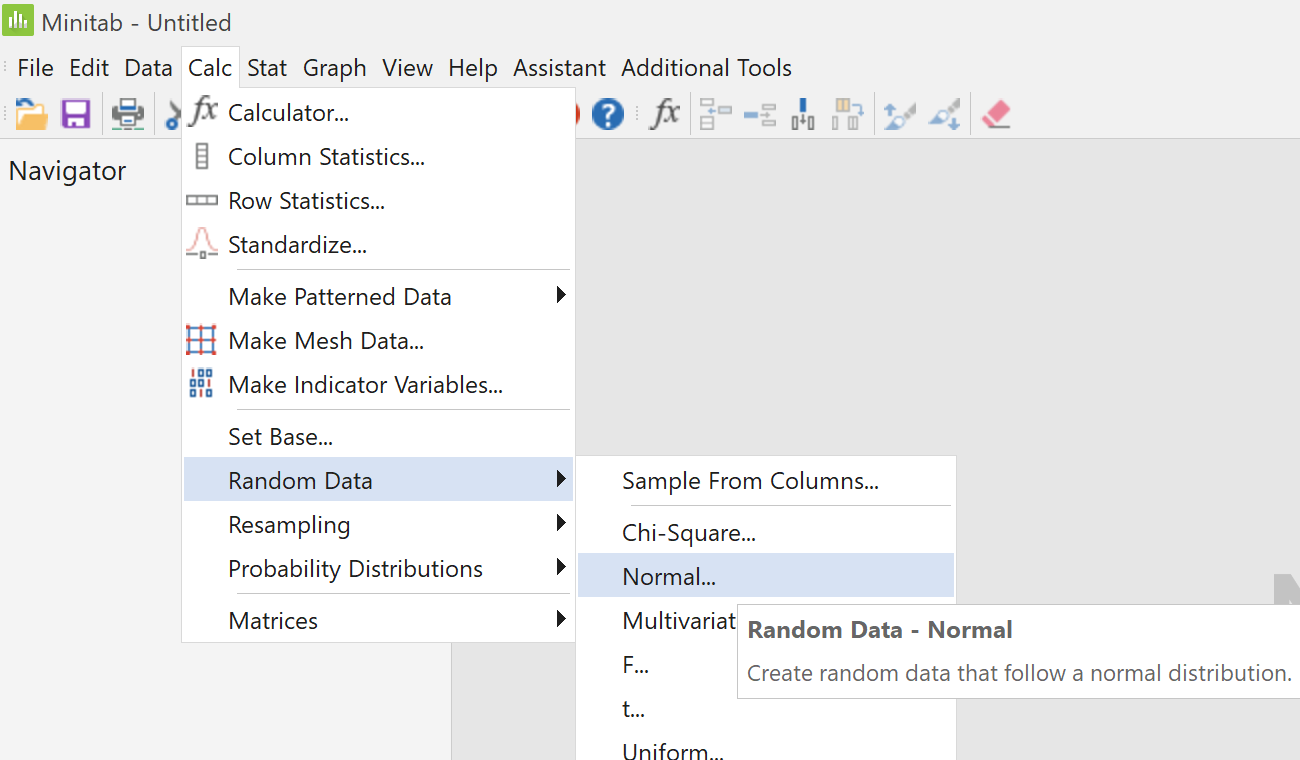
From the "Calc" menu, select "Random Data" then click on "Normal..."


---

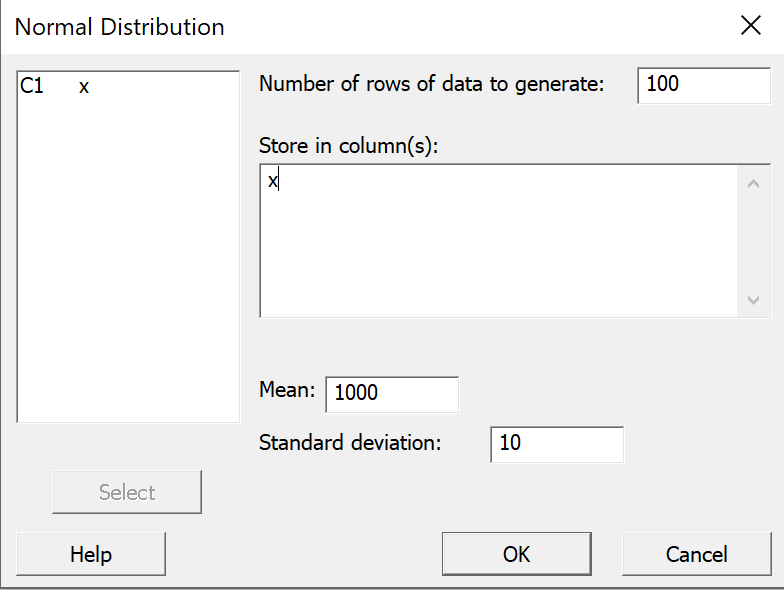
In the dialog box that pops up; enter 100 as the "Number of rows of data to generate"; select x for "Store in column(s)"; enter 1000 for the "Mean"; enter 10 as the "Standard deviation"; and click "OK".

---

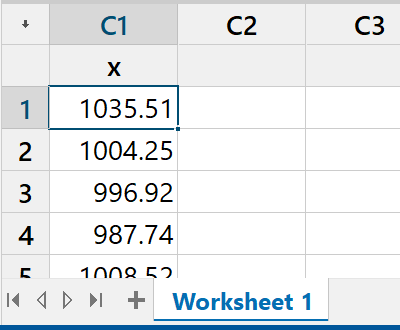
A random sample of 100 values should now appear in column C1 x of the worksheet in the data pane. These values have been drawn randomly from a normal distribution of population mean 1000 and population standard deviation 10

---

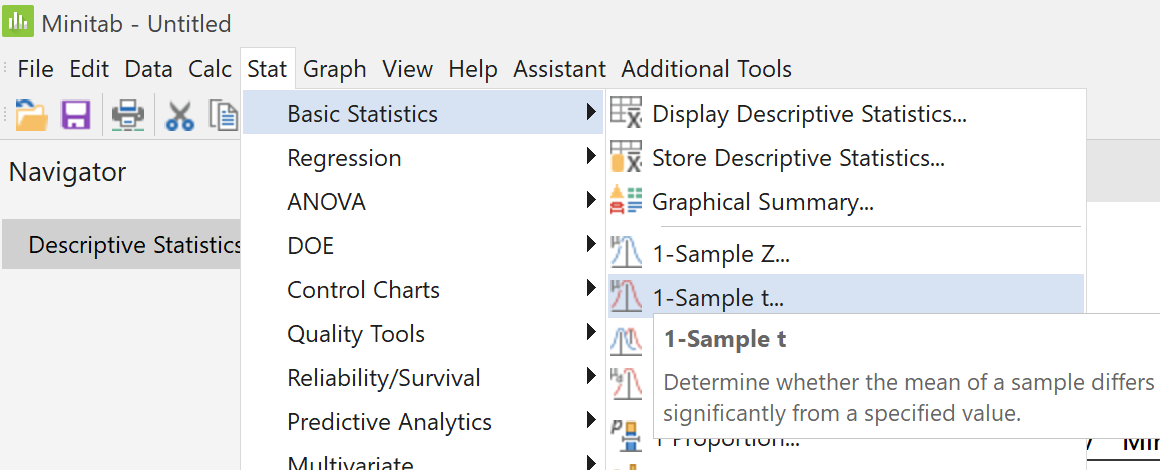
From the "Stat" menu, select "Basic Statistics" then click on "Display Descriptive Statistics..."


---

In the left pane of the dialog box, double click on 'C1 x'. Accept all of the defaults by just clicking "OK".

---

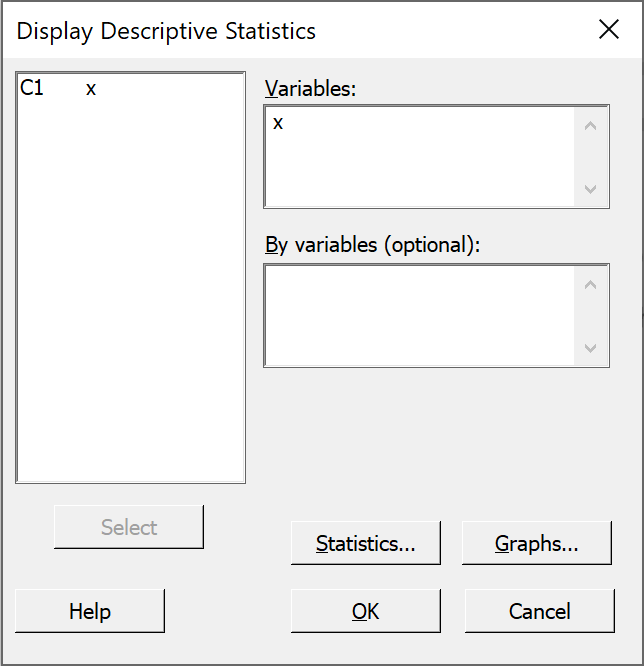
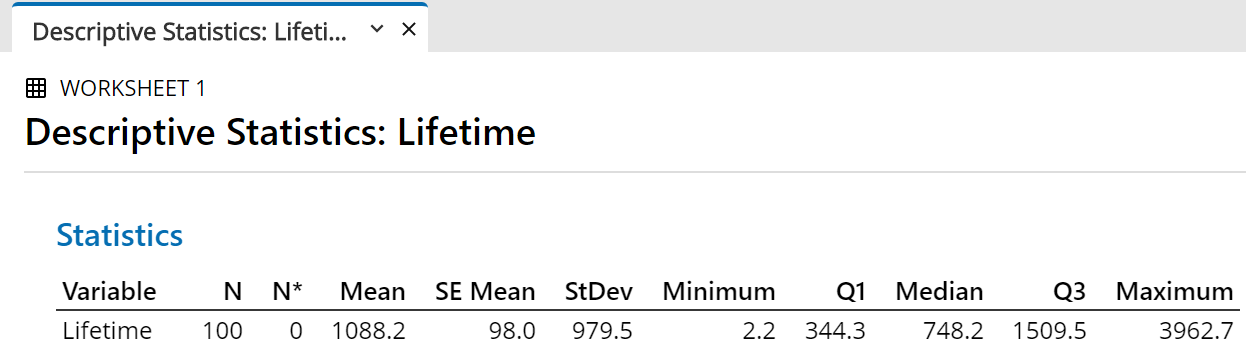
The summary statistics for your random sample then appear in the output pane.
The exact values will vary each time.
The sample mean and sample median are usually close to but not exactly 1000
and the sample standard deviation is usually close to but not exactly 10,
(and therefore the sample standard error is close to ).

 

---

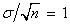Now let Minitab find a 95% two-sided confidence interval for the population mean   µ , based on this random sample.

From the "Stat" menu, select "Basic Statistics" then click on "1-Sample t..."

 

---

In the dialog box "One-Sample t for the Mean" that pops up, Click on the larger right pane. In the left pane the only column with data appears. Double click on C1 x Click on the "Options" button.

---

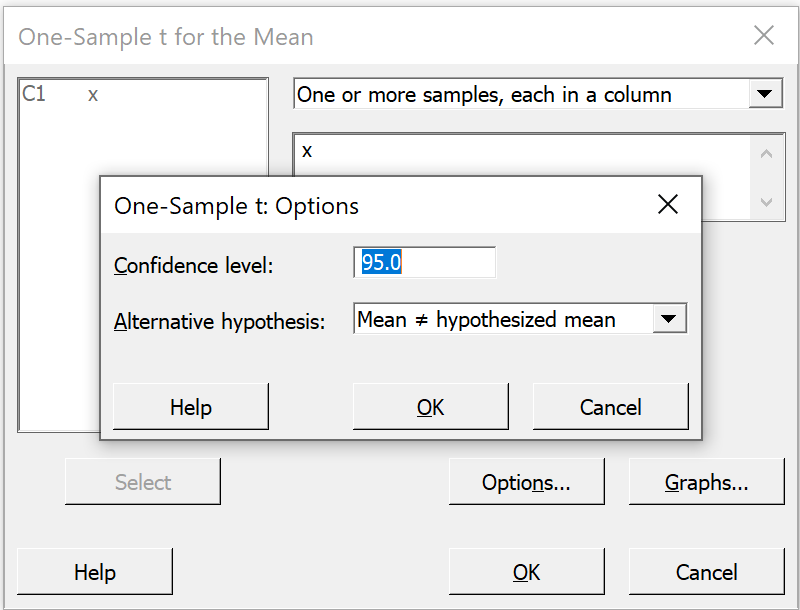
In the secondary pop-up window we see "95.0" for the "Confidence level" and "Mean not= hypothesized mean" (which means a two-sided interval) for "Alternative hypothesis" Just accept these defaults for now and click "OK" on this dialog box, then click "OK" on the first dialog box.

---

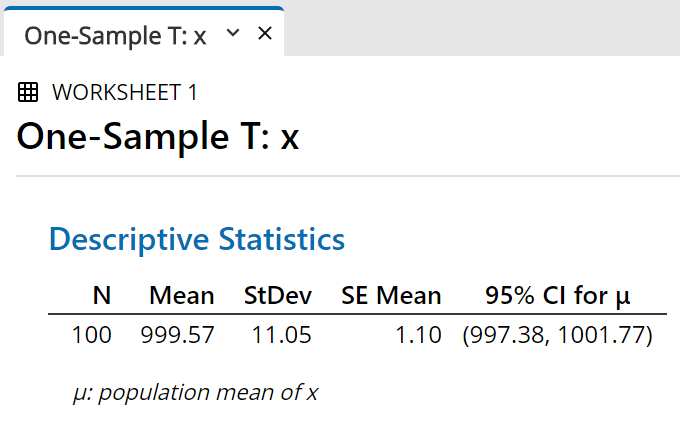
Using the sample mean, the sample size and the sample standard deviation, Minitab constructs a 95% two-sided confidence interval for   µ . The result is displayed in the output pane.

---

We can easily change the level of confidence and/or replace the two-sided interval by a one-sided interval.

---

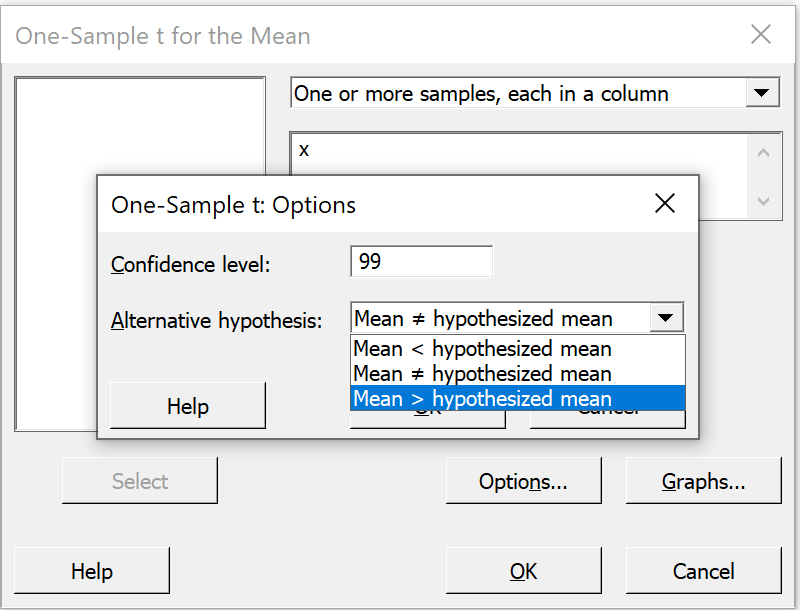
Repeat the steps "Stat" menu   →   select "Basic Statistics"   →   click on "1-Sample t..." In the dialog box "One-Sample t for the Mean" that pops up, Click on the "Options" button. In the secondary pop-up window shown here, change the "Confidence level" from "95.0" to "99.0"; then on the line "Alternative hypothesis", click on the pull-down arrow beside "Mean not= hypothesized mean" and select "Mean > hypothesized mean" instead. Click "OK" on this dialog box, then click "OK" on the first dialog box.

---

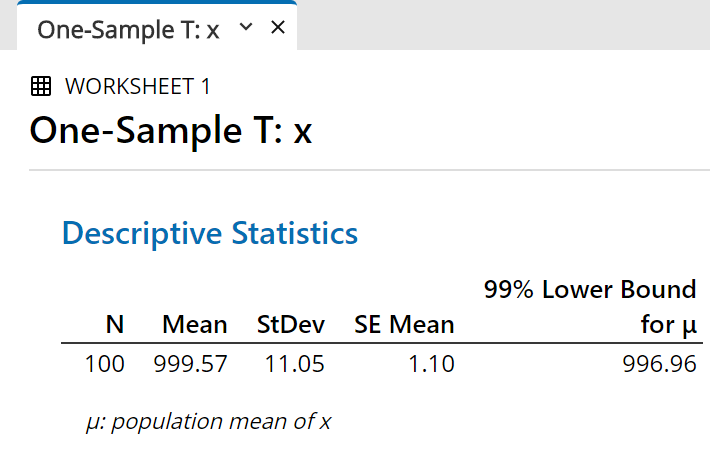
The 99% one-sided confidence interval for   µ  now appears in a new tab in the output pane. Speaking loosely, we are “99% sure that   µ  is greater than” the value shown here (in this illustration, 996.96)

---

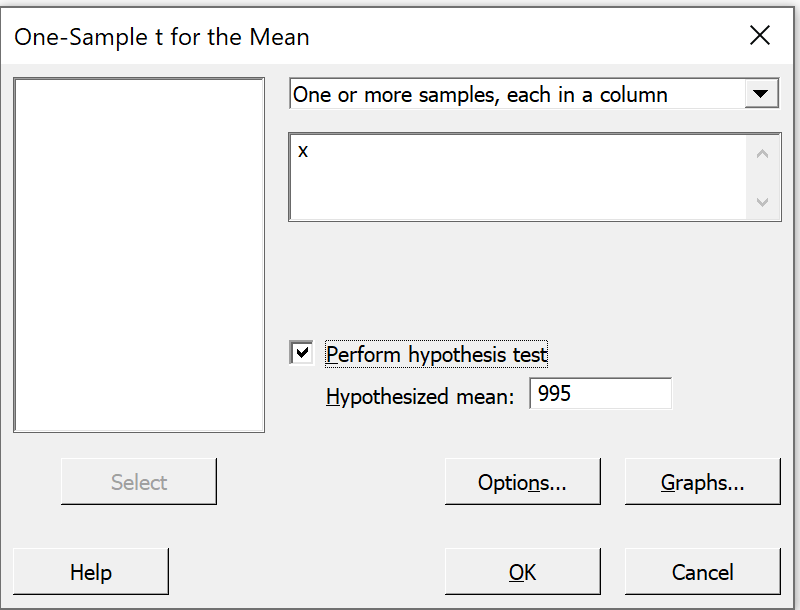
We can also conduct a classical hypothesis test, by repeating the steps above except for checking the box "Perform hypothesis test" and selecting a value for the null hypothesis.

---

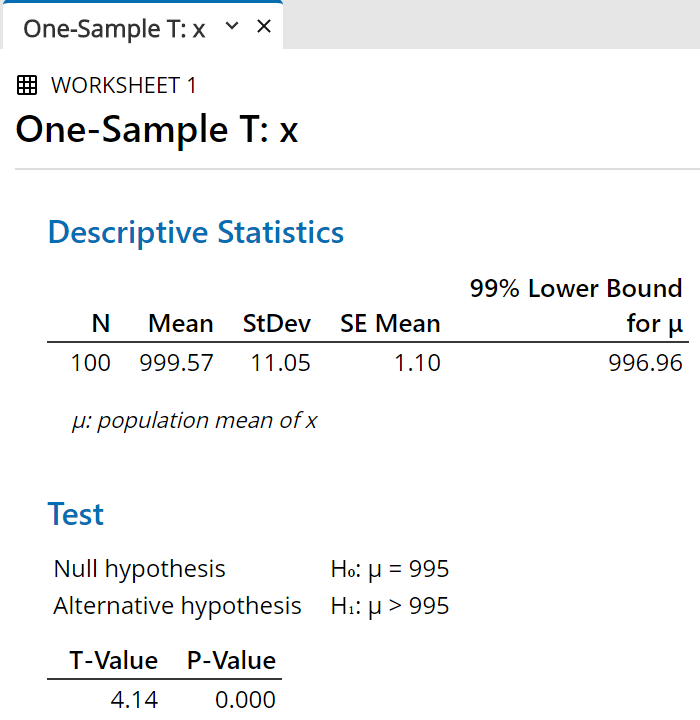
The additional information appears in the output pane, after the confidence interval. The t value can be compared to the appropriate critical t value (Method 2 in class). The P value is the probability that another random sample would produce a sample mean at least as extreme as the one we have, given that the population mean truly is the value that we chose for the "hypothesized mean" in the previous dialog box. In this illustration the P value is less than 0.0005 (which rounds off to 0.000 to three decimal places), so that we are very confident indeed (better than 99.95%) that the true mean is greater than 995. Of course, we know that the true population mean in this case is actually 1000 exactly.

---

You are encouraged to construct both 95% and 99% confidence intervals, two-sided and one-sided, with other data sets.
Assignment #2 requires both a normal probability plot and a one-sided confidence interval.

Also available here is a Minitab macro to simulate the construction of confidence intervals, from many random samples, for a population mean and to show that the proportion of 95% confidence intervals that capture the true value of the population mean is close to 95%.