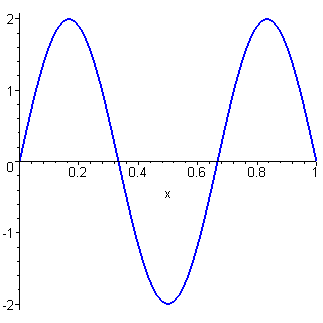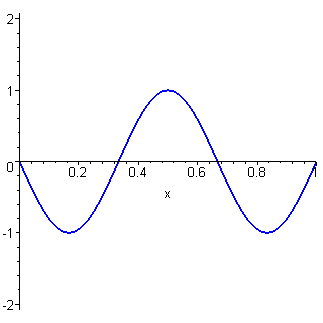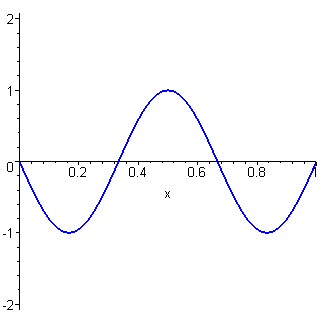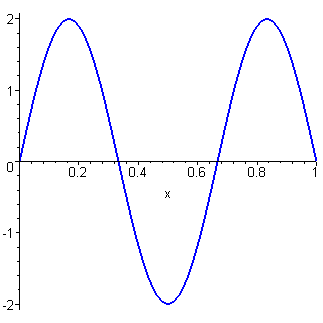
An elastic string is released from rest in a triangular configuration. It is fixed at both ends. The governing partial differential equation is
The complete solution is a Fourier sine series in x:
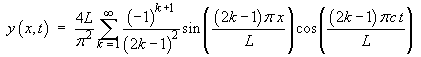
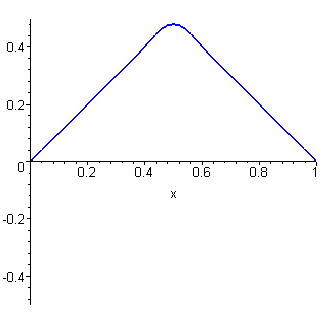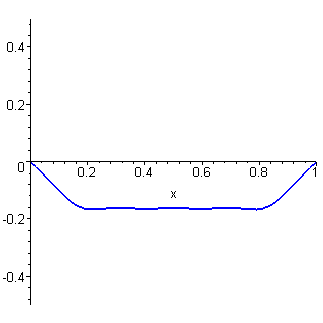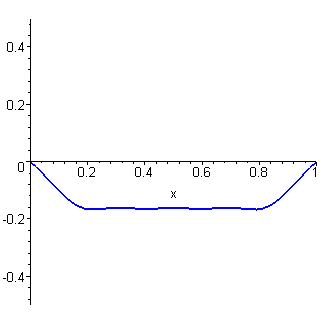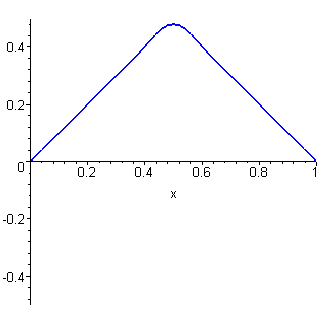
The plot (for c = L = 1) is generated from the first five
non-trivial terms in the Fourier series.
The Maple file is available here.
If the initial configuration is a simple sine function instead
of the triangle function, then the Fourier series collapses to a
single non-zero term.
For example, if 
,
then the complete solution becomes
