A perfectly elastic string of equilibrium length L is released from the initial shape
with an initial velocity profile
The string is clamped at both ends (x = 0 and x = L).
Waves move on the string with speed c.
There is no friction.
Determine the subsequent evolution of the displacement
y(x, t) of the string.
The governing partial differential equation is
The complete solution is the sum of a pair of Fourier sine series
in x.
However, only one term in each series is non-zero (see the lecture notes).
The complete solution is simply
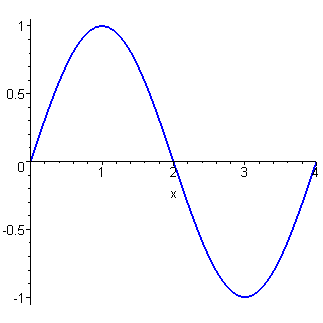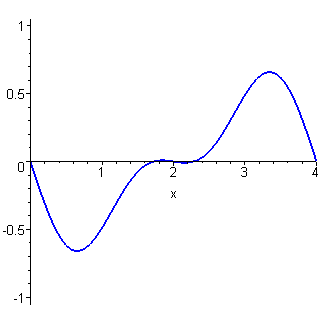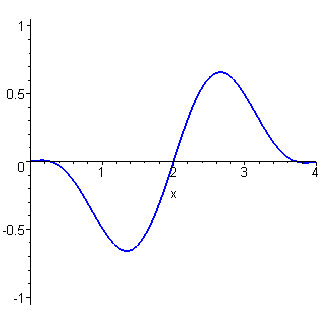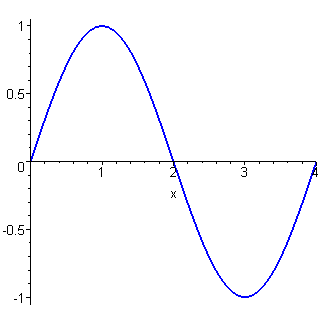
This plot is for L = 4 and c = 1.
The Maple file is available here.
[Return to your previous page]
[Return to the home page for this course]
-
Created 2010 07 15 and most recently modified 2010 07 15 by
Dr. G.H. George