ENGI 5432/5435 Advanced Calculus
Final Examination, 2008 — Questions

  1. Find the Fourier series expansion on the interval (–1, 1) of the function

    f(x) = x^3 - x

    [12]

  1. The vector field   vector F   is defined by   F = < x, 2y, 3z >.

    1. Show that   div F = 6   everywhere in   real space3.

      [3]

    2. Hence evaluate   Phi = closed double integral of F dot dS, where   S   is the surface of the sphere of radius 1 and centre at (0,0,0).   State the name of the theorem that you are using.
      [You may express your answer in terms of p.]

      [7]

  1. In spherical polar coordinates (r, q, f), a scalar function   V   is defined on the domain
    W = { all of real space3 except the z-axis } by

    V(r, q, f)   =   ln (r sin q )

    1. Find   F = gradient of V   in spherical polar coordinates.

      [3]

    2. Express   V   as a function of the Cartesian coordinates (x, y, z) only.

      [3]

    3. Use your answer to part (b) to find   F = gradient of V   in Cartesian coordinates.

      [3]

    4. Show that your answers to parts (a) and (c) are equivalent by using the appropriate coordinate conversion matrix.

      [6]

    5. Find the Laplacian   Laplacian of V   in one of the two coordinate systems.

      [4]

    6. Is   V   harmonic on any domain that excludes the z axis?

      [1]

  1. For the partial differential equation

    u_xx + 5u_xy + 6u_yy = 12

    1. Classify this partial differential equation (as one of hyperbolic, parabolic or elliptic).

      [2]

    2. Find the general solution   u(x, y).

      [5]

    3. Using the additional information

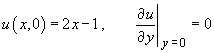
      u(x,0) = 2x - 1 ; u_y(x,0) = 0

      Find the complete solution   u(x, y).

      [10]

  1. Find the equations of the line of force for the vector field   F = < x, y, y^2 >   that passes through the point (1, 1, 1).

    [10]

  1. A vector   vector F   is defined in the cylindrical polar coordinate system by   F = 2 rhoHat - rho phiHat + 4 k.

    1. Find the derivative   vector dF/dt   in terms of   rho, d rho / dt and d phi / dt.

      [5]

    2. Show whether or not a potential function exists for   vector F   and, if it does exist, on what domain.

      [7]

  1. Find the value of the line integral

    W = integ_C { 2(x+y) dx + (2x+2y-1) dy }

    where   C   is the arc of the parabola   y = x2   between (–1, 1) and (1, 1).

    [12]

  1. A shell is in the shape of that part of the ellipsoid   x^2 / 9 + y^2 / 4 + z^2 / 1 = 1 that is above the x-y plane (z > 0).
    Its surface density is   rho = 36z / sqrt{16x^2 + 81y^2 + 1296z^2}
    Find the mass   m   of this shell.
    Note:   For the upper half of the general ellipsoid   x^2 / a^2 + y^2 / b^2 + z^2 / c^2 = 1, a parametric net is (q, f), such that   r = < a sin t cos f, b sin t sin f, c cos t >.
    For the projection method, start with   z = sqrt{ 1 - x^2 / 9 - y^2 / 4 }.
    If necessary, you may quote   Integral of sqrt{a^2 - x^2} = x sqrt{a^2 - x^2} / 2 + a^2 Arcsin(x/a) / 2 + C.
    Either method (parametric net or projection) may be used in this question.

    [7+6]

[Total:   100 marks]

Back to Index of Questions   [Back to the Index of Questions] [On to the Solutions]   To the solution of this exam

Return to your previous page   [Return to your previous page]
Created 2008 04 20 and most recently modified 2008 04 20 by Dr. G.H. George