Problem Set 6   -   Questions

Find the centroid (centre of mass when the surface density is constant) of the frustum of the circular cone   z² = x² + y²   between the origin and the plane   z = a, (where   a   is a positive constant).

Find the total flux that passes through the hemisphere   x² + y² + z² = a²,   z > 0 ,   due to the electric flux density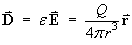 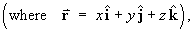    using:

1. the surface projection method   and

2. the parametric surface net method.

3. What can you say about the relative orientation of the vector field D and the normal N to the hemisphere?

Find the total flux of the vector field 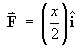through that part of the circular paraboloid   z = 4 - x² - y²   that lies in the first octant.

A thin sheet, in the shape of the paraboloid   z = 16 - (x² + y²), where   x > 0   and   y > 0, has a surface density of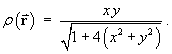     It lies within the coaxial region between the circular cylinders 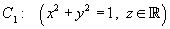    and  

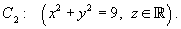
1. Determine the total mass of the sheet, and
2. Locate the centre of mass for the sheet.

Fluid is flowing along a cylindrical pipe.   The circular cross section inside the pipe has a constant radius of a (m).   The Cartesian coordinate system is aligned with the x axis along the line of symmetry (centre line) of the pipe.   The other two axes are in the plane of one of the circular cross sections.   The velocity of fluid at any point (x, y, z) inside the pipe is
             
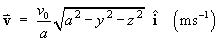
Find the flux   Q (in m³/s)   (the rate at which fluid is flowing through the pipe).

Complete the evaluation (in Example 2.6.3 of the lecture notes) of the line integral 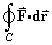    around the unit square in the x-z plane for 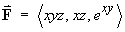, (without using Stokes’ theorem).

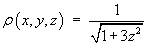
1. using a parametric net method. and
2. using a projection method.