Term Test 1   -   Questions

1. For the ellipsoid defined by  

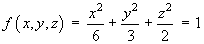
   1. Show that the equation of the tangent plane to the ellipsoid at the point (1, 1, –1) is   x + 2y – 3z = 6.

      [8]

   2. Find, to the nearest degree, the angle that the ellipsoid makes with the plane   z = –1   at the point (1, 1, –1).

      [8]

2. A vector field is defined in cylindrical polar coordinates by .
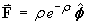   Find   curl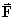   in terms of cylindrical polar components.

   [8]

3. The location 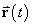of a particle moving in a fluid at any time   t   is given by

   

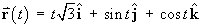
   1. Show that the tangential component of acceleration is zero at all times.

      [5]

   2. Find the radius of curvature   r   at all times.

      [6]

   3. Find the angle between the tangent vector to the path of the particle and the y-z coordinate plane.

      [5]

  BONUS QUESTION

4. Find the equations of the line of force for the vector field 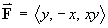    that passes through the point (0, –1, 0).

   [+5]

	[To the Index of Problem Sets.]		[To the solutions to this test]
	[Return to your previous page]