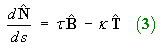ENGI 5432 Advanced Calculus
Faculty of Engineering and Applied Science2009 Winter
Problem Set 1 - Solutions
Let
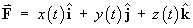 be the position vector of a particle at time t
as it moves along a curve C, where the functions
x(t), y(t) and z(t)
are all differentiable for all values of t.
Show that if
be the position vector of a particle at time t
as it moves along a curve C, where the functions
x(t), y(t) and z(t)
are all differentiable for all values of t.
Show that if 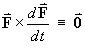 then the particle must always move in the same direction.
then the particle must always move in the same direction.
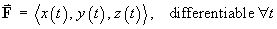
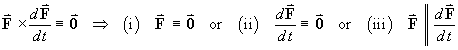
(i) Þ (ii)
(ii) Þ F is a constant vector and the particle is stationary.
But we are told that the particle is moving along a curve C.
Therefore cases (i) and (ii) can be dismissed and
(iii) must be true Þ the velocity vector is parallel to F(t) at all times
Þ F never changes direction.
Therefore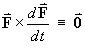 Þ
the particle stays on a straight line path for all time.
Þ
the particle stays on a straight line path for all time.
Let
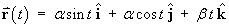 be the position vector of a particle. You may assume that
be the position vector of a particle. You may assume that
 and
and
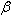 are positive constants.
are positive constants.
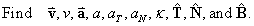
Let s = sin t , c = cos t.
a, b are positive constants.
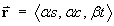
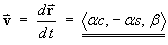
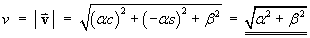
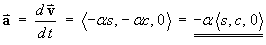
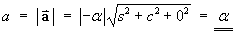
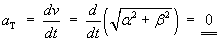 (The speed v is constant)
(The speed v is constant)
or
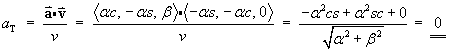
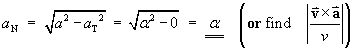
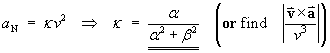
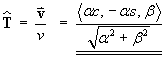
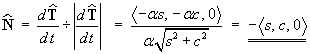
or
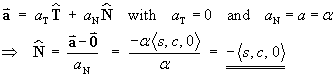
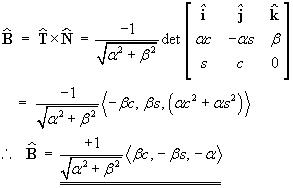
and it is easy to check that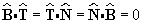
and that || B || = || N || = || T || = 1.- Does the curve lie in one plane?
B is a non-constant function of t (for the x and y components). Therefore
NO, the curve does not lie in one plane. - What type of curve is it?
It is a helix, centred on the z-axis. [The constants a, b in the parametric equation of this curve represent the [constant] magnitude of the acceleration and a measure of the degree to which the helix is stretched out along its axis, respectively.]
There are three formulæ connecting arc length and the unit tangent, unit principal normal and unit binormal vectors, known as the Frenet-Serret formulæ.
Show that the first Frenet-Serret formula is
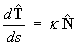 ,
,
where s is arc length and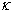 is the curvature.
is the curvature.
By the definition of
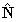 ,
,
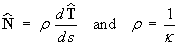
The first formula follows immediately:
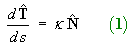
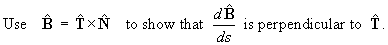
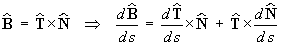
[Note that the cross product is anti-commutative, so the order in which the terms of the derivative by the product rule are written down is important.]
But (1) Þ
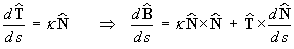
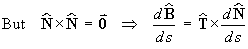 ,
,
which is perpendicular to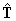 .
.
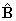 is a unit vector
Þ
is a unit vector
Þ
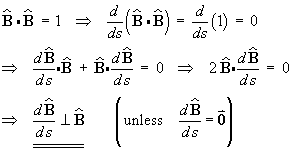
Hence prove the second Frenet-Serret formula
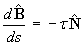 , where the torsion,
, where the torsion,
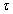 , is some scalar function of
s.
[The torsion is a measure of how much the curve is
twisting out of the plane of
, is some scalar function of
s.
[The torsion is a measure of how much the curve is
twisting out of the plane of
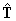 and
and
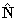 .]
.]
Any vector perpendicular to both
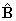 and
and
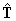 must be ||
must be || 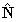 ,
,
(because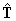 ,
,
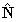 ,
,
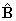 form an orthonormal basis).
form an orthonormal basis).

Define that multiple to be -t (where t = torsion). Then
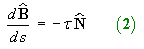
Use the fact that
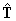 ,
,
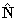 ,
,
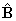 form a mutually orthogonal right-handed triad of unit
vectors, (from which it necessarily follows that
form a mutually orthogonal right-handed triad of unit
vectors, (from which it necessarily follows that
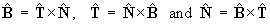 ), to establish the third
Frenet-Serret formula
), to establish the third
Frenet-Serret formula
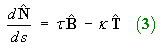
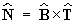 [Cyclic system:
[Cyclic system:
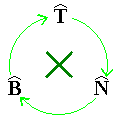 ]
]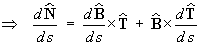
Substitute (1) and (2):
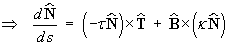
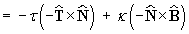 (cross products are anti-commutative)
(cross products are anti-commutative)
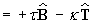
Therefore the third Frenet-Serret formula is