ENGI 5432 Advanced Calculus
Faculty of Engineering and Applied Science2009 Winter
Problem Set 4 - Solutions
- For the vector field

Convert F from Cartesian coordinates to spherical polar coordinates.
Let c1 = cos q , s1 = sin q
c2 = cos f and s2 = sin f , then
x = r s1c2 and y = r s1s2
Þ x2 + y2 = r2s12 (c22 + s22) = r2s12
Þ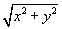 =
r s1
=
r s1
[Note: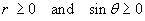 for all values in the spherical polar (r,
q, f) system.
for all values in the spherical polar (r,
q, f) system.
There is therefore no ambiguity in the square root.]
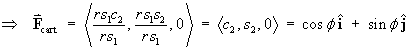
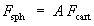
![==> [ Fr ; Ftheta ; Fphi ] = [ s1 ; c1 ; 0 ]](p4/q1a_sol_3.gif)
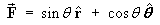
Relative to the coordinate axes, in what direction is F pointing?
![[diagram of F in horizontal plane]](p4/q1b_image1.gif)
 is parallel to the x-y plane everywhere in
is parallel to the x-y plane everywhere in
(except on the z-axis, where F is undefined)In the horizontal plane z = r cos q :
Fy = sin f
Fx = cos f (from part (a) above)
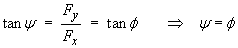
Þ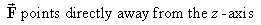
OR
In the vertical plane containing the point P (r, q, f) and the z-axis
(which is the plane f = constant):![[vertical slice showing r and theta components]](p4/q1b_image2.gif) The vertical component of F is
The vertical component of F is
Fr cos q - Fq sin q
= sin q cos q - cos q sin q = 0
Therefore F is parallel to the x-y plane.The azimuthal component (perpendicular into the paper) is
-Fx sin f + Fy cos f
= - cos f sin f + sin f cos f = 0F is therefore in the same vertical plane as the point P and the z-axis.
Þ
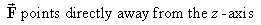
The coordinate conversion matrix A for Cartesian coordinates to spherical polar coordinates is
![[ s1*c2 s1*s2 c1 ]
A = [ c1*c2 c1*s2 -s1 ] c1 = cos theta s1 = sin theta
[ -s2 c2 0 ] c2 = cos phi s2 = sin phi](p4/q2convmat1.gif)
so that Fsph = A Fcart where
![[ F_r ]
F = [ F_theta ] ,
sph [ F_phi ]
F = F_r r^ + F_theta theta^ + F_phi phi^](p4/q2vecsph1.gif)
![[ F_x ]
F = [ F_y ] and
cart [ F_z ]
F = F_x i + F_y j + F_z k](p4/q2veccart1.gif)
Show that the conversion matrix B for the inverse conversion from spherical polar back to Cartesian coordinates, such that
Fcart = B Fsph, is simplyB = AT (the transpose of matrix A).
B = A-1 (because the two transformations are inverses of each other)
In order to show that A-1 = AT, it is sufficient to show that ATA = I.
[This is much faster than the adjoint/determinant method or the row reduction method for finding A-1.]![AT A = [ s1c2 c1c2 (-s2) : s1s2 c1s2 c2 : c1 (-s1) 0 ]
[ s1c2 s1s2 c1 : c1c2 c1s2 (-s1) ; (-s2) c2 0]](p4/q2_sol_1.gif)
![=[ details of matrix multiplication ]](p4/q2_sol_2.gif)
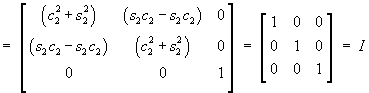
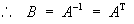 [and the coordinate transformation matrix A is
orthogonal.]
[and the coordinate transformation matrix A is
orthogonal.]
Convert from spherical polar to Cartesian coordinates the vector field
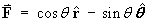
From Question 2, B = AT.
Use the same abbreviations as in questions 1 and 2 :
Let c1 = cos q , s1 = sin q
c2 = cos f and s2 = sin f , then
Fr = c1 , Fq = -s1 , Ff = 0
![==> F(cart) = [ Fx ; Fy ; Fx ]
= [ s1c2 c1c2 (-s2) ; s1s2 c1s2 c2 ; c1 (-s1) 0 ] [ c1 ; (-s1) ; 0 ]](p4/q3_sol_1.gif)
![=[matrix product] = k-hat](p4/q3_sol_2.gif)
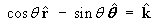
Find the divergence and curl of each of the following:
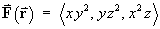
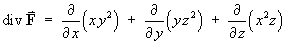
= y2 + z2 + x2 Therefore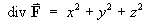
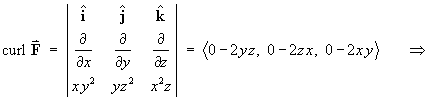
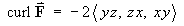
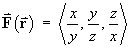
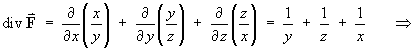
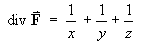
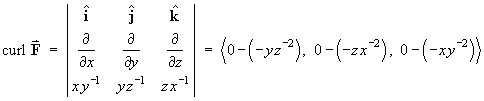
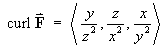
[Note: the cyclic symmetry between x, y, z in parts (a) and (b) above allows any two parts of the calculations for divergence and curl to be deduced from the other part.]
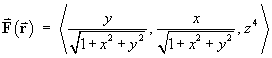
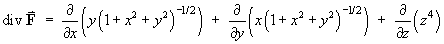
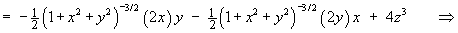
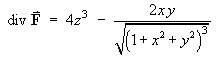
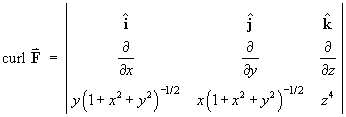
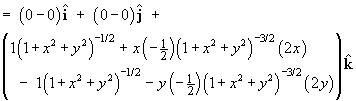
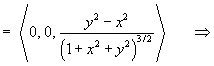
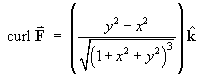
For the vector field defined in spherical polar coordinates by
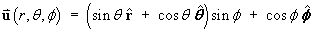
find
 .
.
Recall, from page 1-38 of the lecture notes, that
![[derivative of unit vector rHat]](p4/q5drdt.gif)
![[derivative of unit vector thetaHat]](p4/q5dqdt.gif)
and![[derivative of unit vector phiHat]](p4/q5dfdt.gif)
Use the abbreviations
![[abbreviations]](p4/q5abbrev.gif)
![[abbreviated form of vector u]](p4/q5ushort.gif)
Using the product and chain rules of differentiation,
![[applying the product and chain rules]](p4/q5diff1.gif)
![[gathering up components]](p4/q5diff2.gif)
Therefore, everywhere in space and at all values of t,
OR
Convert the vector u from spherical polar coordinates to Cartesian coordinates:
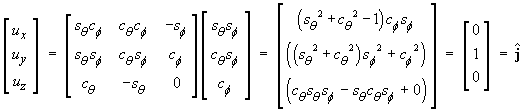
and the derivative of any absolutely constant vector is the zero vector!
Consider the purely radial vector field F (r, q, f) = f (r)
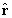 , where
, where
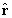 is the unit radial vector in the
spherical polar coordinate system and f (r)
is any function of r that is differentiable everywhere
in
is the unit radial vector in the
spherical polar coordinate system and f (r)
is any function of r that is differentiable everywhere
in  (except possibly at the origin).
(except possibly at the origin).- Find an expression, in terms of r,
f (r) and f ' (r), for
the divergence of F.
First note that f (r) is a function of r only, so that
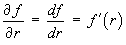
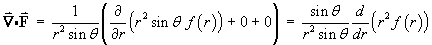
Therefore, everywhere except possibly on the z axis,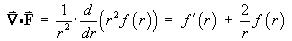
- Find an expression, in terms of r,
f (r) and f ' (r), for
the curl of F.
![[curl in determinant form for spherical polar]](p4/q6bcurl1.gif)
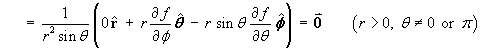
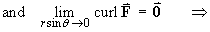
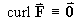
[All purely radial differentiable vector fields are therefore automatically irrotational.]
Of particular interest is the central force law
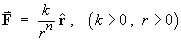
Show that the divergence of F vanishes everywhere in
 (except possibly at the origin) if and only if
(except possibly at the origin) if and only if
n = 2 .
[Two of the four fundamental forces of nature, electromagnetism and gravity, both obey this inverse square law.]
![[Substitute f(r) into part (a)]](p4/q6csubst.gif)
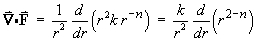
div F therefore vanishes for all r > 0 if and only ifn = 2 . [Note: n = 2 recovers the familiar inverse square law,
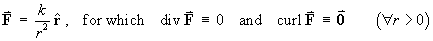 ]
]
- Find an expression, in terms of r,
f (r) and f ' (r), for
the divergence of F.