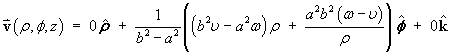ENGI 5432 Advanced Calculus
Faculty of Engineering and Applied Science2009 Winter
Problem Set 8 - Solutions
[Sections 1.7, 2.6, 3]A point charge Q at the origin gives rise to the electrostatic potential field
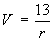
- the potential V at the point
(x, y, z ) =
(3, -4, 12).
(x, y, z) = (3, -4, 12) Þ r2 = 9 + 16 + 144 = 169
Þ r = 13 . Therefore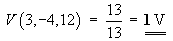
- the electric field vector E at the
point
(x, y, z ) =
(3, -4, 12).
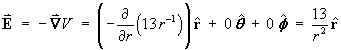
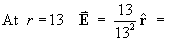
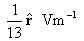
- the volume charge density
rV at the point
(x, y, z ) =
(3, -4, 12).
[Hint: use Poisson’s equation div D = rV .]
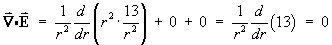

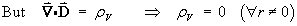
Therefore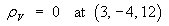
- the magnitude Q of the point charge
at the origin.
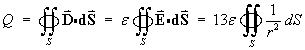
where S is any sphere, centre O, radius r.
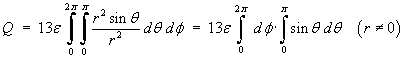
![= 13e [phi]_0^2pi [-cos theta]_0^pi
= 13e 2pi (1+1)](p8/q1d3.gif)
Therefore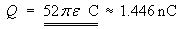
or
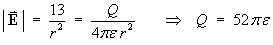
- the potential V at the point
(x, y, z ) =
(3, -4, 12).
In spherical polar coordinates, the scalar field V is defined by
V(x, y, z) = r cos2q . - The vector field F is defined by
F = ÑV .
Find F.
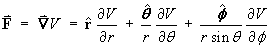
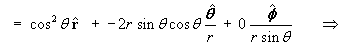
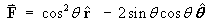
- Find the divergence of F.
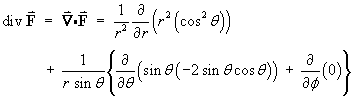
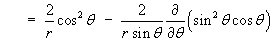
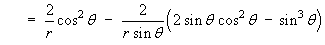
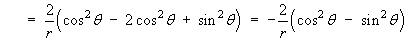
Therefore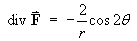
Note that the divergence of F is also the Laplacian of V :
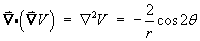
- Find the curl of F.
[Long method:]
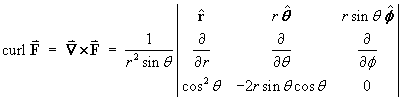
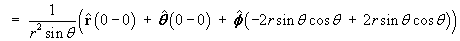
Therefore (except possibly on the z axis)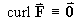
[It can be shown that the curl remains the zero vector as one approaches any point on the z axis in the limit from any direction.]
[Short method:]
F is the gradient of a scalar function V.
A quotable identity is curl grad V º 0 for all twice-differentiable scalar fields V.
Therefore curl F º 0 .
- The vector field F is defined by
F = ÑV .
Find F.
For the scalar field
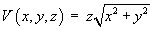
- Find ÑV
in the Cartesian coordinate system.
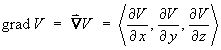
Note that
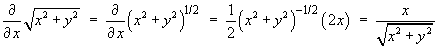
Using symmetry, it then follows that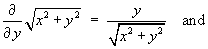
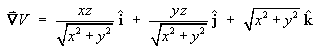
- Find the Laplacian
Ñ2V
in the Cartesian coordinate system in simplified form.
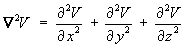
Using the quotient rule:
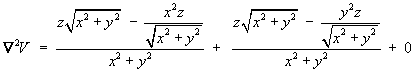
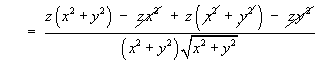
Therefore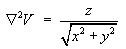
[Also note that (Laplacian of V) = div grad V .]
- Convert V(x, y, z) to spherical
polar coordinates.
x = r sin q cos f
y = r sin q sin f
z = r cos q
Þ x2 + y2 = r2 sin2q (cos2f + sin2f) = (r sinq)2
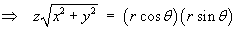
Therefore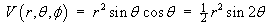
- Find ÑV in the
spherical polar coordinate system in simplified form.
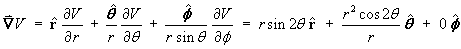
Therefore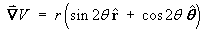
This is equivalent to
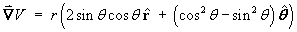
- Show that the Laplacian
Ñ2V
in the spherical polar coordinate system is
cot q.
Either use (Laplacian of V) = div grad V, or quote the spherical polar form for the Laplacian:
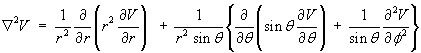
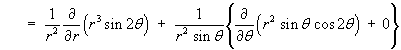
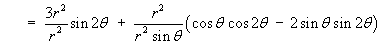
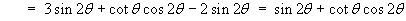
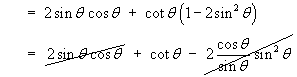
ThereforeÑ2V = cot q - Hence show that the value of the Laplacian of V is
the same in both coordinate systems (except possibly on
the z-axis).
From part (c), z = r cos q and x2 + y2 = (r sinq)2
From part (b),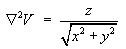
Therefore
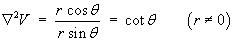
which is the spherical polar form found in part (e).
- Find ÑV
in the Cartesian coordinate system.
A set of functions {fn(x) } is said to be orthonormal on the interval
(a, b) if
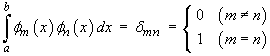
Show that { sin npx }, { cos npx } are both orthonormal on the interval(-1, 1). [Note: It then follows that if
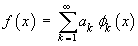 then
then
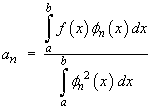 which leads to methods of series solution of
differential equations, including Fourier series.]
which leads to methods of series solution of
differential equations, including Fourier series.]
The following trigonometric identities are quotable:
sin A sin B º ( cos(A-B) - cos(A+B) ) / 2
andcos A cos B º ( cos(A+B) + cos(A-B) ) / 2
Therefore
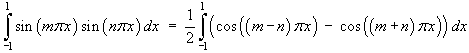
If m ¹ n then
![Int_-1^1 sin m*pi*x sin n*pi*x dx =
(1/2) [sin(m-n)pi*x / (m-n)pi - sin(m+n)pi*x / (m+n)pi]_-1^1](p8/q402.gif)
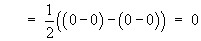
[Note that m + n cannot be zero because both m and n are positive.]If m = n then
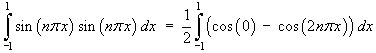
![= (1/2) [x - sin 2n*pi*x / (2n*pi)]_-1^1
= (1/2) ((1-0) - (-1-0)) = 1](p8/q405.gif)
Therefore { sin np x } is an orthonormal set of functions on (-1, 1).
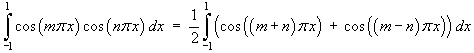
If m ¹ n then
![Int_-1^1 cos m*pi*x cos n*pi*x dx =
(1/2) [sin(m+n)pi*x / (m+n)pi + sin(m-n)pi*x / (m-n)pi]_-1^1](p8/q407.gif)
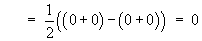
If m = n then
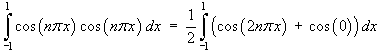
![= (1/2) [sin 2n*pi*x / (2n*pi) + x]_-1^1
= (1/2) ((0+1) - (0-1)) = 1](p8/q410.gif)
Therefore { cos np x } is an orthonormal set of functions on (-1, 1).
[One can also show that every member of the set
{ cos mp x } is orthogonal to every member of the set{ sin np x } on(-1, 1).]
Find the Fourier series for the function f (x) defined on the interval
[–1, 1] by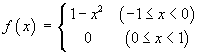
![[graph of y = f(x)]](p8/q5graph1.gif)
L = 1
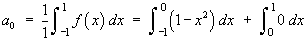
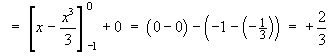
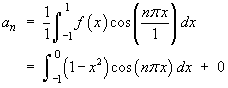
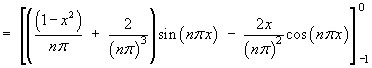
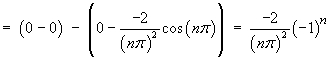
![[tabular integration by parts]](p8/q5parts1.gif)
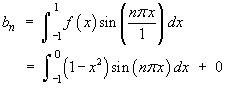
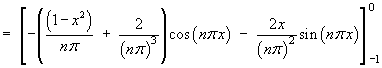
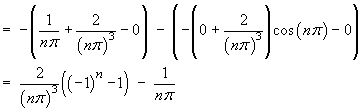
![[tabular integration by parts]](p8/q5parts2.gif)
The Fourier series of f (x) on [–L, +L] in general is
![[general Fourier series]](p8/q5j.gif)
Therefore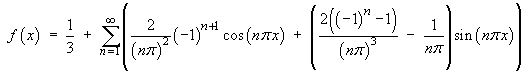
The first few terms of this series are
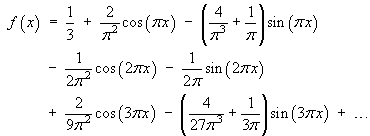
The convergence is quite slow, due to the discontinuity at x = 0 and the abrupt change in slope at the ends of the interval, as this graph of the fourth partial sum S4 illustrates:![[graph of S4 and f(x)]](p8/q5graph2.gif)
y = f (x) is in red
y = S4 is in cyan.
Find the Fourier series for the function f (x) defined on the interval
[–1, 1] by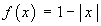
![[graph of y = f(x)]](p8/q6graph1.gif)
L = 1
f (x) is even Þ bn = 0 for all n.
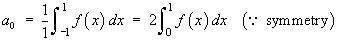
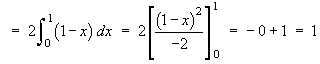
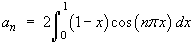
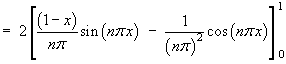
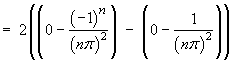
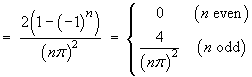
![[tabular integration by parts]](p8/q6parts.gif)
Therefore the Fourier series is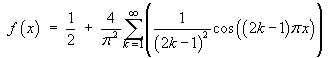
The first few terms of this series are
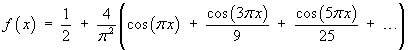
The partial sum of just the first three non-zero terms yields an impressively good approximation everywhere except near the points wheref (x) is not differentiable:![[graph of y = f(x)]](p8/q6graph2.gif)
y = f (x) is in red
y = S3 is in blue.
Find the Fourier cosine series for the function f (x) defined on the interval
[0, 2] by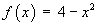
![[graph of y = f(x)]](p8/q7graph1.gif)
L = 2
An even extension of f (x) is required
bn = 0 for all n.
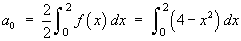
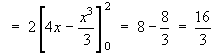
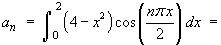
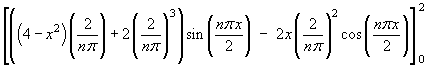
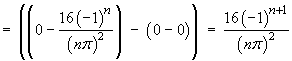
![[tabular integration by parts]](p8/q7parts.gif)
Therefore the Fourier series is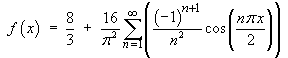
The first few terms of this series are
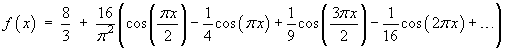
The partial sum of the first four terms yields a fair approximation everywhere except near the endpoints, wheref (x) is not differentiable:![[graph of y = f(x)]](p8/q7graph2.gif)
y = f (x) is in red
y = S3 is in blue.
Find the Fourier sine series for the function f (x) defined on the interval
[0, 2] by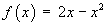
Also comment on why the rate of convergence of this Fourier series everywhere in the interval
[0, 2] is much more rapid than in question 7.
![[graph of y = f(x)]](p8/q8graph1.gif)
L = 2
An odd extension of f (x) is required.
an = 0 for all n.Note how the periodic extension of f (x) is not only continuous everywhere but differentiable everywhere, even at the endpoints. We therefore anticipate a more rapid convergence than in question 7.
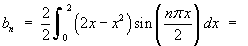
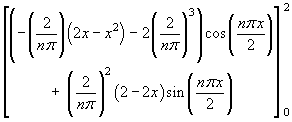
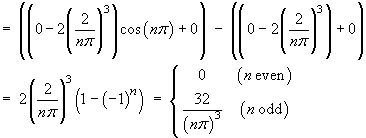
![[tabular integration by parts]](p8/q8parts.gif)
Therefore the Fourier series is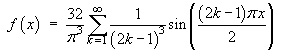
The first few terms of this series are
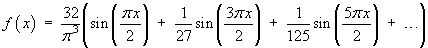
The partial sum of just the first two non-zero terms yields an excellent approximation everywhere:![[graph of y = f(x)]](p8/q8graph2.gif)
y = f (x) is in red
y = S3 is in blue.
[A more challenging question:]
An incompressible viscous fluid is in steady-state flow around the z-axis, trapped between a pair of coaxial rotating cylinders, aligned along the z-axis. The inner cylinder has radius a and rotates at angular velocity w k. The outer cylinder has radius b (> a) and rotates at angular velocity u k.
In response, the velocity vector at any point in the fluid, in cylindrical polar coordinates(r, f, z), is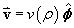 and v(r)
obeys the ordinary differential equation
and v(r)
obeys the ordinary differential equation
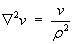
Where it is in contact with a cylinder, the fluid must move with the same velocity as that cylinder.
Solve the ODE to find the velocity at all points in the fluid.
The Laplacian of any scalar function V in cylindrical polar coordinates is, in general,
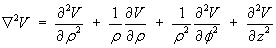
However, the velocity vector has neither radial nor vertical components.
The f component of the velocity vector is a function of r only, so that the ODE becomes
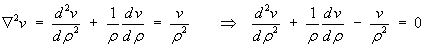
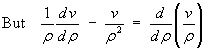 so that the ODE becomes
so that the ODE becomes
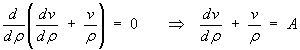
This is a linear first order ODE and can be solved by that method,
or one may use a similar shortcut to an exact form again:
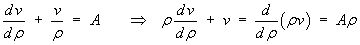
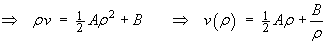
The two arbitrary constants are determined by the two boundary conditions.
The linear speed of each cylinder is just the product of the radius of that cylinder with its angular speed:
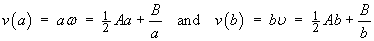
![[eliminating A]](p8/q9j.gif)
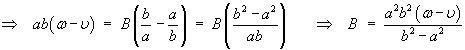
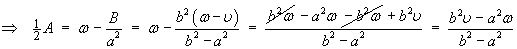
The complete solution for the velocity vector at any point (r, f, z) in the fluid is therefore