ENGI 5432 Advanced Calculus
Faculty of Engineering and Applied Science2009 Winter
Problem Set 9 - Solutions
- Is the function f (x, y )
= 3 x2y
-
y3 harmonic and, if so,
on what domain?
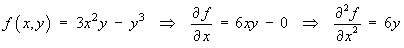
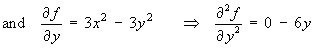
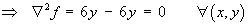
ThereforeYES, f (x, y ) is harmonic on all of 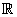 2.
2.
- Find the subsequent motion of an infinite string that
is released from rest with the initial displacement
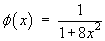
Release from rest Þ q (x) º 0.
The d’Alembert solution
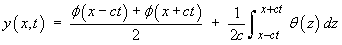
is therefore
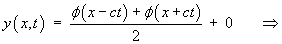
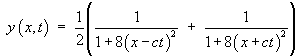
![[Maple animation of this wave]](p9/q2maple.gif)
- Classify the partial differential equation
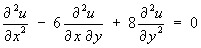
and find its complete solution, given the additional information
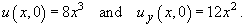
A = 1 , B = –6 , C = 8 Þ D = 36 - 4(8) = 4 > 0
Thereforethe PDE is hyperbolic. This is a homogeneous second order linear PDE with constant coefficients, for which the d’Alembert method may be used to find a general solution.
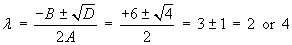
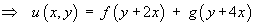
Applying the additional information:
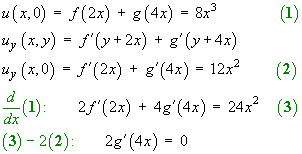

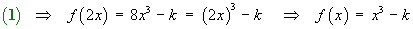
The complete solution is therefore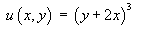
- Classify the partial differential equation
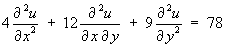
and find its complete solution, given the additional information
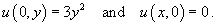
A = 4 , B = 12 , C = 9 Þ D = 144 - 4(4)(9) = 0
Thereforethe PDE is parabolic. 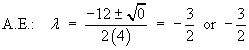
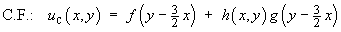
where h(x, y) is any non-trivial linear function of x and y that is not a multiple ofy + lx.
A simple choice, such as h(x, y) = x , will do.
Therefore one form of the complementary function is
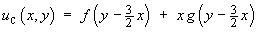
The right side function is a constant (78), while the left hand side involves only second partial derivatives. The particular solution must therefore be some function of x and y of second order only, so we try
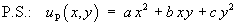
The second partial derivatives of this trial particular solution are
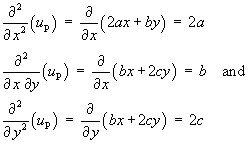
Substituting into the PDE we obtain
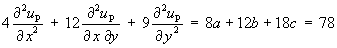
There is only one condition on the three constants.
We therefore have a free choice for two of the constants.
Choose b = 0 and c = a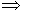 26a = 78
26a = 78
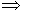 a = 3
a = 3
The particular solution is therefore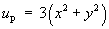
and the general solution is
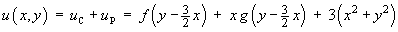
In order to find the complete solution, we employ the additional information:
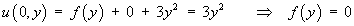
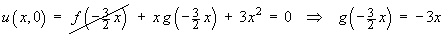
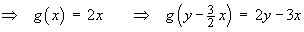
The complete solution to the PDE is therefore
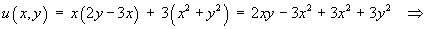
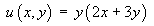
- Classify the partial differential equation
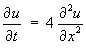 and find its complete solution on the interval
and find its complete solution on the interval
0 < x < 100 for all positive time t, given the additional information
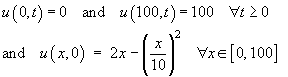
Also write down the steady state solution.
t is playing the role of y.
A = 4 , B = 0 , C = 0 Þ D = 0 - 4(4)(0) = 0
This is also the PDE for heat diffusion. Thereforethe PDE is parabolic. From page 4.28 of the lecture notes (Example 4.5.1), the complete solution of the heat equation (with the boundary conditions of constant temperatures T1 and T2 at the ends
x = 0 andx = L respectively and an initial temperature profile on[0, L] ofu(x, 0) = f (x) ) is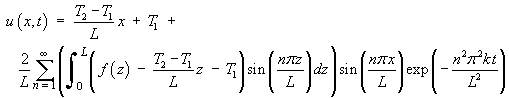
In this case k = 4, L = 100, T1 = 0, T2 = 100 and f (x) = 2x – (x/10)2.
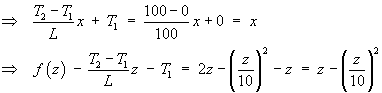
The coefficients in the Fourier sine series become
![[Integral for Fourier sine series coefficients]](p9/q5d.gif)
![[Evaluation of Integral]](p9/q5e.gif)
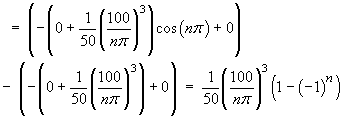
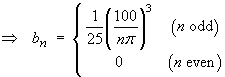
Integration by parts:
![[table for integration by parts]](p9/q5parts.gif)
Also 2/L = 1/50. After some simplification of constants and substitution of(2k – 1) for the index of summation n, the complete solution becomes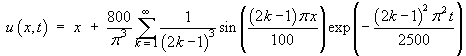
![[Maple animation of the evolution of the temperature]](p9/q5animation.gif)
The Fourier series for x converges rapidly.
The steady state solution is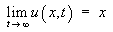
Two snapshots of u (x, t):
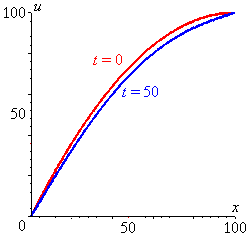
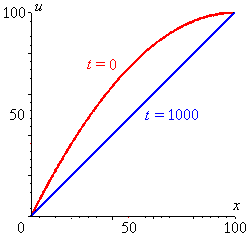
[The Maple file used to generate these diagrams is available here.]
- Classify the partial differential equation
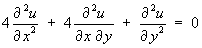 and find its general solution.
and find its general solution.
A = 4 , B = 4 , C = 1 Þ D = 16 - 4(4) = 0
Thereforethe PDE is parabolic. 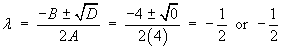
Assume a complementary function of the form
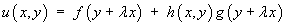
where h(x, y) is any non-trivial linear function of x and y that is not a multiple ofy + lx.
A simple choice, such as h(x, y) = x , will do.
Therefore one form of the general solution is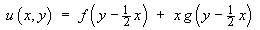
The functional forms of f and g remain arbitrary in the absence of any further information (such as boundary conditions). Several alternatives are possible, such as
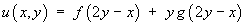 .
.
- Classify the partial differential equation
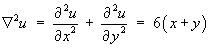 and find its general solution.
and find its general solution.
A = 1 , B = 0 , C = 1 Þ D = 0 - 4(1) = -4 < 0
Thereforethe PDE is elliptic. Assuming a complementary function of the form uC = f (ax+by) + g(ax+by),
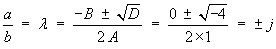
Þ uC(x, y) = f (y - jx) + g(y+jx)Many possibilities exist for the particular integral. Among them is:
Try uP(x, y) = c (x3 + y3)
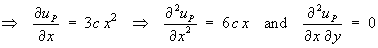
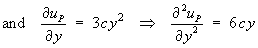
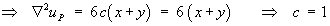
Therefore the P.I. is uP(x, y) = x3 + y3
and the general solution isu(x, y) = f (y - jx) + g(y+jx) + x3 + y3 The functional forms of f and g remain arbitrary in the absence of any further information (such as boundary conditions).