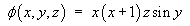ENGI 5432 Advanced Calculus

    Faculty of Engineering and Applied Science
    2009 Winter

    Examples for Potential Functions

      In each case, find the potential function for the vector field,
      (or prove that no such potential function exists).

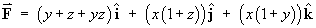
    1. F = < y+z+yz, x(1+z), x(1+y) >

      We are seeking a potential function   f (x, y, z)   such that
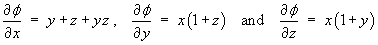
      df/dx = y+z+yz, df/dy = x(1+z) & df/dz = x(1+y)
      It is often helpful to start with the most complicated component, in this case the x component.   f   must include a term
      xy + xz + xyz
      Checking the other two partial derivatives,
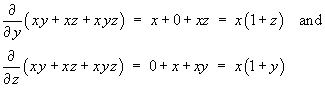
      df/dy = x+xz & df/dz = x+xy
      which is completely consistent.   Therefore the potential function must be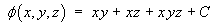

      phi = xy + xz + xyz + C

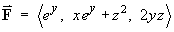
    1. F = < e^y, x e^y + z^2, 2yz >

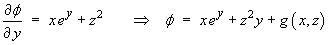
      df/dy = x e^y + z^2 ==> f = x e^y + y z^2 + g(x,z)
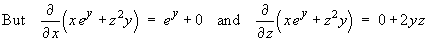
      df/dx = e^y and df/dz = 2yz
      which matches the components of F exactly.   Therefore the potential function is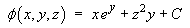

      phi = x e^y + y z^2 + C

    1. F = < -y, x, z >

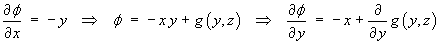
      df/dx = -y ==> f = -xy + g(y,z)
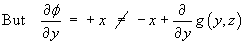
      df/dy = x not= -x + g'(y,z)
      We have an inconsistency, which suggests that no potential function exists.
      [g (y, z)   must be a function of y and z only, not of x.]
      Checking for the existence of a potential function:
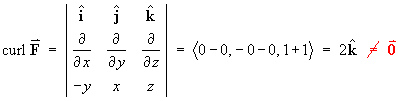
      curl F not= zero vector
      which confirms that, for this vector field F,

        no potential function exists.  

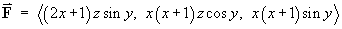
    1. F = < (2x+1)z sin y, x(x+1)z cos y, x(x+1) sin y >
      and the potential is zero on all coordinate planes.

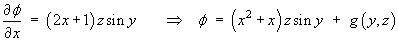
      df/dx = (2x+1)z sin y ==> f = (x^2 + x)z sin y + g(y,z)
      [df/dy and df/dz match]
      which matches the components of F exactly.   The potential function is
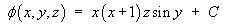
      phi = x(x+1)z sin y + C
      When any one or more of x, y, z is zero, f = C.
      The condition that the potential be zero on the coordinate planes leads to C = 0.
      Therefore the potential function is

      phi = x(x+1)z sin y + C

          Return to the Index of Problem Set Solutions   [To the Index of Solutions.]
          Back to previous page   [Return to your previous page]
    Created 2008 02 25 and most recently modified 2008 12 27 by Dr. G.H. George