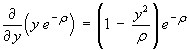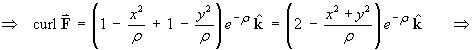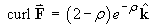ENGI 5432/5435 Advanced Calculus

    Faculty of Engineering and Applied Science
    2008 Winter

    Term Test 1 Question 2
    Alternative Solution

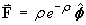    1. A vector field is defined in cylindrical polar coordinates by rho exp(-rho) phiHat.
      Find   curl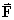 vector F   in terms of cylindrical polar components.

      [illustration of relationship between cylindrical polar and Cartesian coordinates] Express the polar basis vector in its Cartesian form:
      phiHat = -sin phi iHat + cos phi jHat
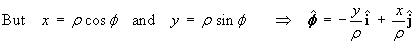
      x = rho cos phi, y = rho sin phi ==> phiHat = -y/rho iHat + x/rho jHat
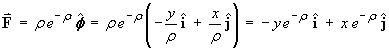
      F = exp(-rho) < -y, x, 0 >
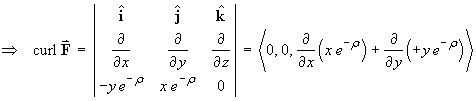
      curl F = ...
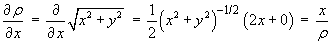
      partial drho/dx = x/rho
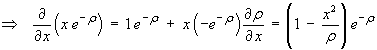
      partial d/dx {x exp(-rho)} = (1 - x^2/rho) exp(-rho)
      By symmetry, partial d/dy {y exp(-rho)} = (1 - y^2/rho) exp(-rho)
      curl F = (2 - (x^2 + y^2)/rho) exp(-rho) kHat

      curl F = (2 - rho) exp(-rho) kHat

    Return to the Solutions to Term Test 1, Winter 2008   [Return to Term Test 1 Solutions.]
    Back to previous page   [Return to your previous page]

    Created 2008 01 27 and most recently modified 2008 01 27 by Dr. G.H. George