ENGI 5432 Advanced Calculus
Faculty of Engineering and Applied Science2009 Winter
Term Test 1 - Solutions
For the surface defined by
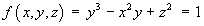 ,
,- Find the equations of the tangent plane and the normal
line to the surface at the point
(–1, 1, 1).
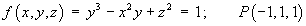
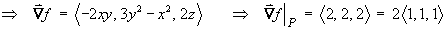
The vectors defining the tangent plane are
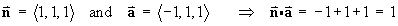
The equation of the tangent plane is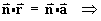
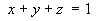
The vectors defining the normal line are
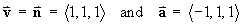
The equation of the line is
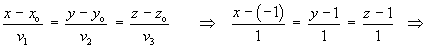
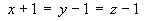 [or z = y = x + 2]
[or z = y = x + 2] - Find, to the nearest degree, the angle that the surface
makes with the plane
x + z = 0 at the point(–1, 1, 1).
The angle between the surface and the plane is also the angle between the normal of the tangent plane to the surface at that point and the normal to the plane
x + z = 0 .
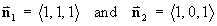
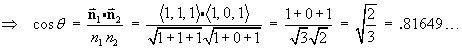
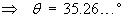 Correct to the nearest degree,
Correct to the nearest degree,q = 35°
- Find the equations of the tangent plane and the normal
line to the surface at the point
The location of a particle is defined in spherical polar coordinates by
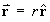 .
.
At any instant,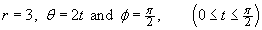 .
.
Find the velocity v in spherical polar coordinates.
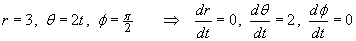
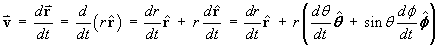
![[only one non-zero term for the velocity]](t1/q2e09.gif)
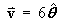
A thin wire is in the shape of the unit circle in the xy-plane,
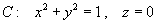 ,
which can be parameterized by .
,
which can be parameterized by .
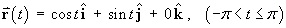 .
.
The line density of the wire is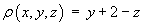 .
.- Find the mass and the Cartesian coordinates of
the centre of mass of the wire.
![[circular wire]](t1/wire09.gif)
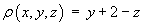
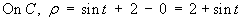
The element of mass for the wire is
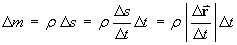
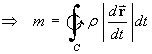
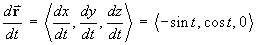
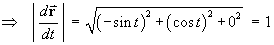
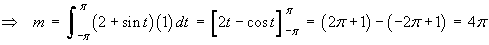
The wire lies entirely in the xy-plane
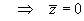
Both the wire and the density are symmetric about x = 0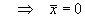
The wire is symmetric about y = 0, but the density is not.
Taking moments about the xz plane,
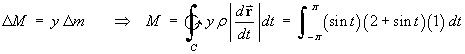
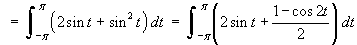
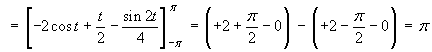
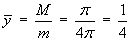
Therefore the mass and centre of mass of the wire are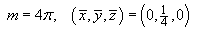
Note that, without consideration of symmetry, the evaluation of the vector moment would have been
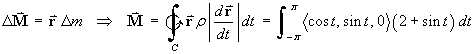
- Find the work done by a force
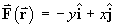 in travelling once around the wire.
in travelling once around the wire.
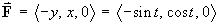
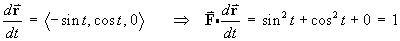
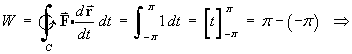
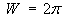
- Find the mass and the Cartesian coordinates of
the centre of mass of the wire.
For the velocity field
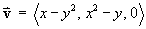
- Find the divergence div v.
![[divergence]](t1/q4a109.gif)
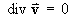
BONUS QUESTION
- Find the stream function
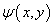 and the family of streamlines for v.
and the family of streamlines for v.
z never changes and
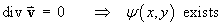
![[match partial derivatives of psi]](t1/q4b309.gif)
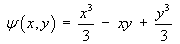
and the family of streamlines is
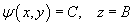
or, re-writing the family as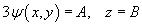
the family of streamlines is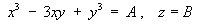
The family of streamlines is plotted on this separate page.
- Find the equation of the streamline that passes through
the point
(2, 0, 0).
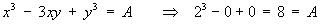
Also z = 0 leads obviously to B = 0.
Therefore the required streamline is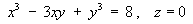
- Find the divergence div v.