ENGI 9420 Engineering Analysis
Faculty of Engineering and Applied Science
2008 Fall
Final Examination Questions
-
- Find the inverse of the matrix
![[ 1 0 0 ]
[-1 1 1 ]
[-1 0 -1 ]](f08/q1a1.gif)
[9]
Hence (or otherwise) solve the following problem:
The frictional force F (in units of Newtons =
kg m s–2) on a spherical body of radius
a (m) falling with speed
v (m s–1) through a viscous
liquid of viscosity
h
(kg m–1 s–1)
is of the form
 ,
where k, x, y and z
are dimensionless constants. Find the values of
x, y and z.
,
where k, x, y and z
are dimensionless constants. Find the values of
x, y and z.
[7]
A pair of simultaneous first order ODEs is defined by
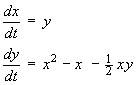
- Find both critical points of this system of first order ODEs.
[3]
- Determine the nature and stability of both critical points.
[6]
- Sketch the phase portrait for the linear approximation to
the non-linear system in the neighbourhoods of both
critical points.
[Note: the general solution is not
required.]
[6]
- Hence sketch the phase portrait for the original non-linear
system.
[5]
An initial value problem is defined by
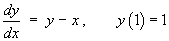
Use the standard fourth order Runge-Kutta method, with
a step size of h = 0.2, to find the
value at x = 1.2 of the solution of
this initial value problem.
[9]
- Verify your solution to part (a) by solving the initial
value problem analytically.
[7]
-
Find the path y = f (x) between
the points (0, 1) and (1, 1) for which the integral
![I = Integral[0 to 1] { 12xy + (y')^2 } dx](f08/q4integral.gif)
has an extremum and determine whether the extremum
is a maximum or a minimum.
[16]
BONUS QUESTION
- If the integrand F (x, y,
y' ) is a function of y'
only, then it follows that the extremal path is
the straight line joining the endpoints, unless
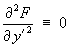 .
Show that, if
.
Show that, if
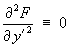 ,
then the integral
,
then the integral
![I = Integral[x0 to x1] { F(y') } dx](f08/q4b2.gif) has the same value, no matter what path
y = f (x) is taken between
the fixed points
has the same value, no matter what path
y = f (x) is taken between
the fixed points
 and
and
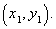
[+6]
Sketch the graph of the odd periodic extension of the
function
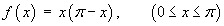
and find its Fourier half-range sine series
expansion.
[16]
A cylinder containing a viscous fluid is rotating at a
constant angular speed
wo .
The fluid moves with a velocity (in the cylindrical polar
coordinate system) of
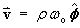
- Find the divergence of the velocity vector.
[7]
- Find the curl of the velocity vector.
[6]
- Find
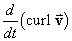
[3]
[Also provided with this examination paper were three
pages from the lecture notes on stability analysis,
together with the formulae for the RK4 method,
the Euler equation for extremals, simple Fourier series and
the divergence and curl in general orthogonal curvilinear coordinates.]
 [Index of Questions]
[Go to the Solution of this Exam]
[Index of Questions]
[Go to the Solution of this Exam]
 [Return to your previous page]
[Return to your previous page]
Created 2008 12 17 and most recently modified 2008 12 17 by
Dr. G.H. George.
![[ 1 0 0 ]
[-1 1 1 ]
[-1 0 -1 ]](f08/q1a1.gif)
 ,
where k, x, y and z
are dimensionless constants. Find the values of
x, y and z.
,
where k, x, y and z
are dimensionless constants. Find the values of
x, y and z.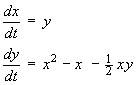
![I = Integral[0 to 1] { 12xy + (y')^2 } dx](f08/q4integral.gif)
![I = Integral[x0 to x1] { F(y') } dx](f08/q4b2.gif) has the same value, no matter what path
y = f (x) is taken between
the fixed points
has the same value, no matter what path
y = f (x) is taken between
the fixed points