ENGI 9420 Engineering Analysis

Faculty of Engineering and Applied Science
2006 Fall

Final Examination Questions

  1. Use the method of Gaussian elimination to find the inverse of the matrix

    [ 1 0 2 ] [ 1 1 1 ] [ 3 2 5 ]

    [16]

  1. The second order ordinary differential equation

    x" + 3x' + 2x – x^2 = 0

    may be represented by the linked pair of first order ODEs

      dx/dt = y ; dy/dt = x^2 – 2x – 3y

      1. Find all of the critical points of this system of first order ODEs.

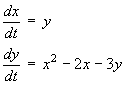
        [2]

      2. Determine the nature and stability of the critical points.

        [5]

      3. Find the general solution to the linear approximation to the non-linear system in the neighbourhood of the origin (x, y) = (0, 0) only.

        [5]

      4. Sketch the phase portrait for the the linear approximation to the non-linear system in the neighbourhood of the origin (x, y) = (0, 0) only.

        [4]

      BONUS QUESTION

      1. Sketch the phase portrait for the non-linear system in a region that includes all critical points.

        [+6]

    1. An initial value problem is defined by

      dy/dx = x + y , y(–1) = 1

      1. Use the standard fourth order Runge-Kutta method, with a step size of h = 0.2, to find the value at x = –0.8 of the solution of this initial value problem.

        [10]

      2. Verify your solution to part (a) by solving the initial value problem analytically.

        [6]

    1. Find the extremal   y(x)   for the integral

      I = Integral[1 to 2] { (1 + y')^2 / (2x + 1) } dx

      that passes through the points (1, 1) and (2, 4).

      [16]

    1. Find the Fourier series expansion of the function

      f(x) = 1 – abs(x) , (abs(x) <= 1)

      [20]

    1. For the vector field   F = –100 / r^2 rHat, where   r = < x, y, z >,

      1. find the curl of F.

        [8]

      2. find the divergence of F.

        [8]

    [Also provided with this examination paper were three pages from the lecture notes on stability analysis, together with the formulae for the fourth order Runge-Kutte method, the Euler equation for extremals, simple Fourier series and the divergence and curl in Cartesian coordinates.]

    Return to the index of assignments   [Index of Questions]               [Go to the Solution of this Exam]   Go to the Solution of this Exam
    Return to your previous page   [Return to your previous page]

    Created 2006 12 14 and most recently modified 2006 12 14 by Dr. G.H. George.