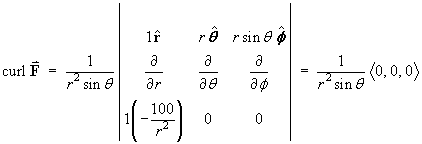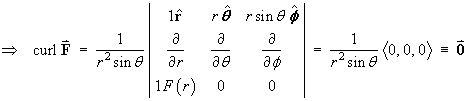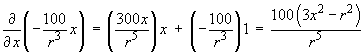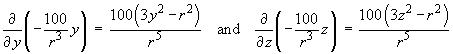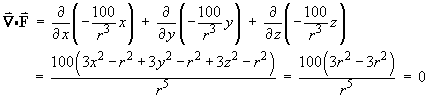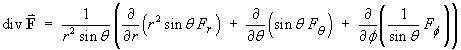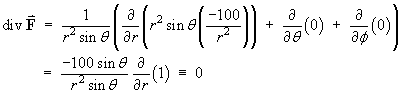find the curl of F.
Cartesian method:
First, note that
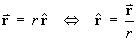
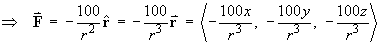
Also note that
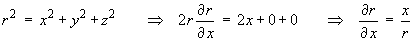
and, by symmetry,
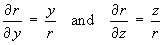
By the chain rule,
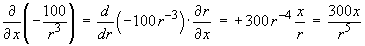
and, by symmetry,
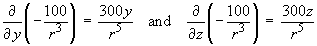
![curl F = [determinant] = vector 0](ff06/q6a7.gif)
OR
Spherical
Polar Method:
F is a purely radial vector field:
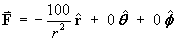
The scale factors in spherical polar coordinates are:
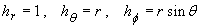
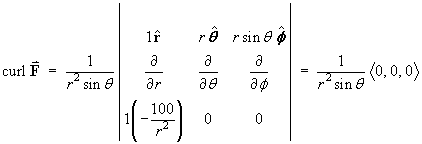
Therefore
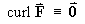
Note that any spherically symmetric vector field,
(that is, a vector field whose magnitude depends only
on the distance from the origin and whose direction
everywhere is directly towards or directly away from the
origin only), is necessarily irrotational:
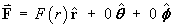
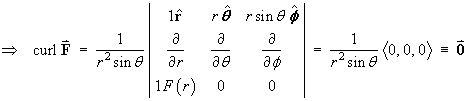
find the divergence of F.
Cartesian method:
By the results in part (a), together with the product rule
of differentiation,
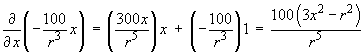
and, by symmetry,
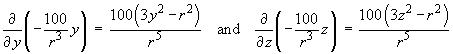
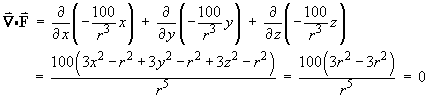
OR
Spherical Polar Method:
For the general vector field
For the vector field in this question, we have
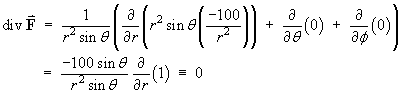
Therefore
[Note that the inverse square law central force
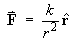 has zero divergence and is therefore
free of sources and sinks everywhere (except
possibly at the origin).]
has zero divergence and is therefore
free of sources and sinks everywhere (except
possibly at the origin).]
![[ 1 0 2 ]
[ 1 1 1 ]
[ 3 2 5 ]](ff06/q1a.gif)
![[ 1 0 2 | 1 0 0 ]
[ 1 1 1 | 0 1 0 ]
[ 3 2 5 | 0 0 1 ]](ff06/q1b.gif)
![[reduced augmented matrix]](ff06/q1c.gif)
![[reduced augmented matrix]](ff06/q1d.gif)
![[I | A^(-1)]](ff06/q1e.gif)
![A^(-1) =
[ 3 4 -2 ]
[ -2 -1 1 ]
[ -1 -2 1 ]](ff06/q1f.gif)
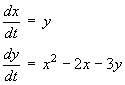
![[ 0 1 ]
[ 2a-2 -3 ]](ff06/q2b1.gif)
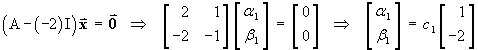
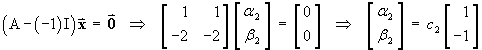
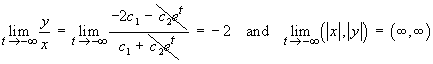
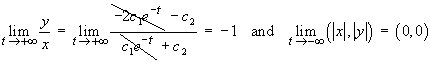
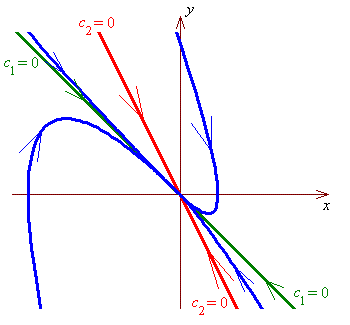
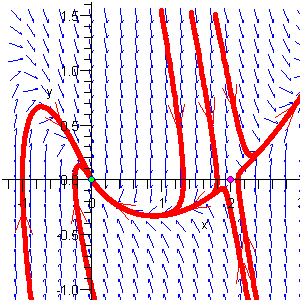
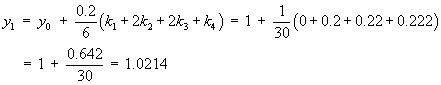
![I = Integral[1 to 2] { (1 + y')^2 / (2x + 1) } dx](ff06/q4integral.gif)
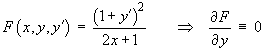
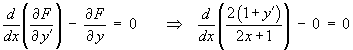
![[substitute into general solution]](ff06/q4e.gif)
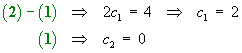
![[graph of f(x), showing symmetry]](ff06/q5graph1.gif)
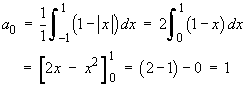
![[Integral]](ff06/q5e.gif)
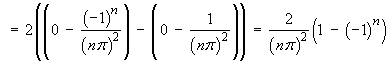
![[tabular integration by parts
of (1 - x) cos(n pi x) ]](ff06/q5parts.gif)
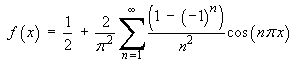
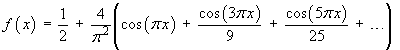
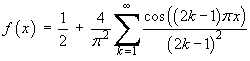
![[graph of f(x) and its Fourier series partial sum]](ff06/q5graph2.gif)
![curl F = [determinant] = vector 0](ff06/q6a7.gif)