ENGI 9420 Engineering Analysis
Faculty of Engineering and Applied Science
2007 Fall
Final Examination Questions
Use the method of Gaussian elimination to solve the
linear system
![[ 1 1 1 | 0 ]
[ 2 3 2 | 1 ]
[ 3 2 -2 | 5 ]
[ 6 6 1 | 6 ]](f07/q1a.gif)
[16]
A pair of simultaneous first order ODEs is defined by
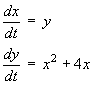
- Find both critical points of this system of first order ODEs.
[3]
- Determine the nature and stability of both critical points.
In particular, provide a reason why it is likely that one
of the critical points of the non-linear system
is a centre (not a focus).
[6]
- Sketch the phase portrait for the linear approximation to
the non-linear system in the neighbourhoods of both
critical points.
[6]
- Hence sketch the phase portrait for the original non-linear
system.
[5]
BONUS QUESTION
- Find the equation of the separatrix and add it to
your sketch in part (d). Note on your sketch the
exact values of the x axis intercepts for the separatrix.
[+6]
A function f (x) is defined by
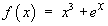
- Show that f ' (x) > 0 for
all x.
It then follows that f (x) = 0
has a unique solution.
[3]
- Use Newton’s method to find the solution to
f (x) = 0 correct to four
decimal places.
Justify your choice of an initial guess
x0.
[13]
Find the path y = f (x) between
the points (0, 1) and (1, 1) for which the integral
![I = Integral[0 to 1] { 2x + 3y + (y')^2 } dx](f07/q4integral.gif)
has an extremum and determine whether the extremum
is a maximum or a minimum.
[16]
Find the Fourier series expansion of the function
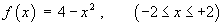
[16]
An arbitrary purely radial vector field F may be
defined in spherical polar coordinates by
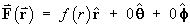 ,
where f (r) is some
differentiable function of the distance r
from the origin.
,
where f (r) is some
differentiable function of the distance r
from the origin.
- Show that any purely radial vector field is irrotational
(that is,
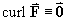 ).
).
[4]
- Show that, in order for the divergence of F to be zero
everywhere, f (r) must
be inversely proportional to the square of the distance
from the origin.
[12]
[Also provided with this examination paper were three pages from the
lecture notes on stability analysis, together with the formulae for
Newton’s method, the Euler equation for extremals,
simple Fourier series and the
divergence and curl in general orthogonal curvilinear coordinates.]
 [Index of Questions]
[Go to the Solution of this Exam]
[Index of Questions]
[Go to the Solution of this Exam]
 [Return to your previous page]
[Return to your previous page]
Created 2007 12 13 and most recently modified 2007 12 13 by
Dr. G.H. George.
![[ 1 1 1 | 0 ]
[ 2 3 2 | 1 ]
[ 3 2 -2 | 5 ]
[ 6 6 1 | 6 ]](f07/q1a.gif)
![[ 1 1 1 | 0 ]
[ 2 3 2 | 1 ]
[ 3 2 -2 | 5 ]
[ 6 6 1 | 6 ]](f07/q1a.gif)
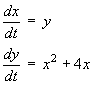
![]()
![I = Integral[0 to 1] { 2x + 3y + (y')^2 } dx](f07/q4integral.gif)
![]()
![]() ,
where f (r) is some
differentiable function of the distance r
from the origin.
,
where f (r) is some
differentiable function of the distance r
from the origin.