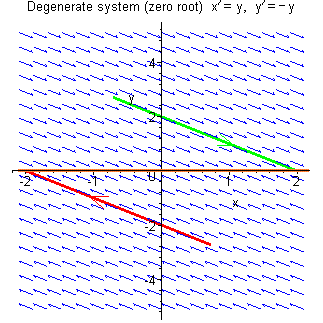
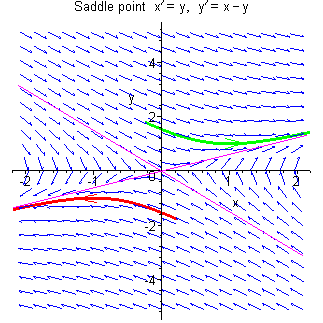
On this page is a demonstration of the effect of varying the parameters of a linear system so that its eigenvalues evolve from a complex conjugate pair with negative real part (leading to a point singularity at the origin which is a stable focus), through to an equal real negative pair (stable node with asymptote parallel to the tangent at the origin), then to a distinct real negative pair (stable node with asymptote not parallel to the tangent at the origin), then to one eigenvalue zero and the other negative (a degenerate system where all trajectories are parallel straight lines terminating on the x axis and where the point singularity has been stretched out into an infinite line), and finally to a pair of real eigenvalues of opposite sign (saddle point).
In each case, the trajectory through the point (1, 1) is
highlighted in green and the trajectory through
The linear system used in this demonstration is
![]()
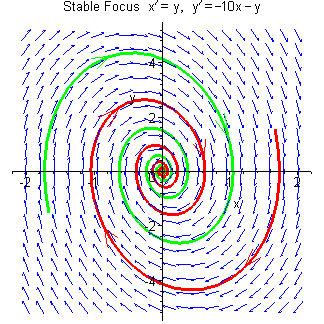
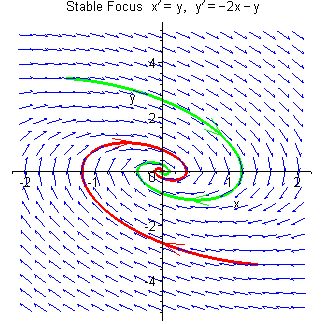
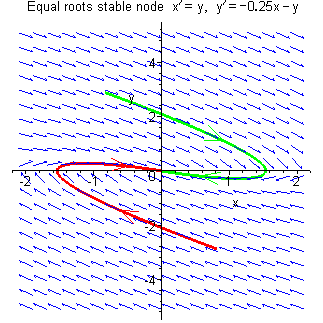
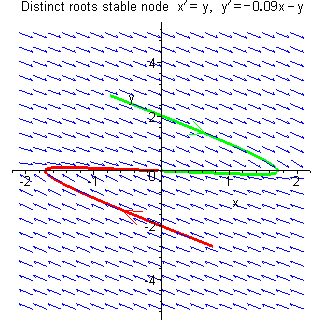
In summary, the nature of the linear system
![]()
for various values of a is:
| Value of a | Type of singularity |
|---|---|
| a < –1/4 | Asymptotically stable focus |
| a = –1/4 | Asymptotically stable improper node |
| –1/4 < a < 0 | Asymptotically stable proper node |
| a = 0 | Degenerate [line] singularity |
| a > 0 | Unstable saddle point |
The Maple file used to generate these images is available here.