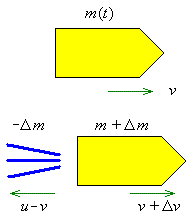
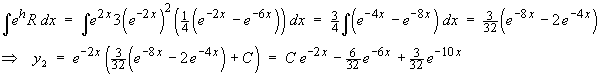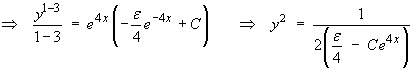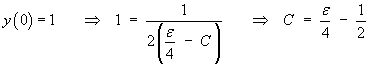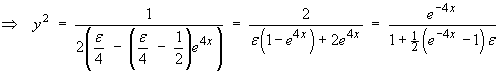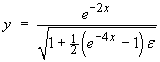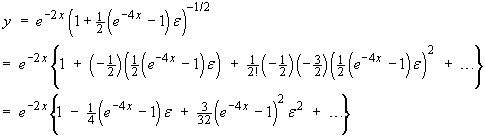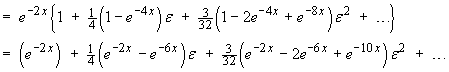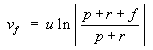ENGR 9420 Engineering Analysis
Mid Term Test Solutions

2006 Fall

  1. Find the complete solution to the initial value problem

    (y^2 – y) dx + (xy – x) dy = 0 , y(1) = 1

    Py = 2y - 1, Qx = y - 1 not= Py therefore not exact
    (Py - Qx) / Q not a function of x only
    Therefore an integrating factor does not exist as a function of x only.
    (Qx - Py) / P = -1 / (y-1) = R(y)
    integrating factor = 1 / (y-1)
    The exact ODE is therefore
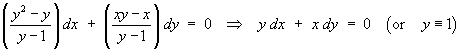
    y dx + x dy = 0 or y = 1
    Following the non-singular solution,
    u = xy = c
    c = 1
    However, note that the singular solution   y = 1   is also consistent with the initial condition   y(1) = 1 .
    Therefore the complete solution is

    y = 1/x or y = 1

    [One could spot the common factor of (y – 1) initially, take note of the singular solution, then divide the ODE by it to leave the much simpler separable ODE   y dx + x dy = 0 .   Separation of variables then leads to a rapid solution.]

  1. The response   x(t)   of a shock absorber to a sudden blow may be modelled by the initial value problem

    x" + 2x' + 17x = 4 delta(t-5) , x(0) = x'(0) = 0

    where   d (t – a)   is the Dirac delta function.
    Using any valid method, find the response   x(t).

    Let X(s) = Laplace transform of solution
    (s^2 + 2s + 17) X = 4 exp(-5s)
    X = L{exp(-t) sin 4t} exp(-5s)
    By the second shift theorem, the complete solution is

    exp(-(t-5)) sin 4(t-5) H(t-5)

  1. Find a power series solution about   x = 0   of the ordinary differential equation

    x^2 y" + 5x y' + 3y = 0

    using the method of Frobenius.

    x Q/P = 5, x^2 R/P = 3, F/P = 0
    x = 0 is therefore a regular singular point of this ODE.
    Attempt a Frobenius series solution.
    y = Sum c_n x^(n+r)
    Substitute this series into the ODE:
    Sum c_n [(n+r)(n+r-1) + 5(n+r) + 3] x^(n+r) = 0
    Sum c_n [(n+r)^2 + 4(n+r) + 3] x^(n+r) = 0
    Sum c_n [(n+r+1)(n+r+3)] x^(n+r) = 0
    The leading term (n = 0) is
    r = -1 or -3
    [Setting   c0 = 0   leads to the trivial solution   y = 0.]

    At   r = –1 , the series becomes
    c0 arbitrary; all other cn = 0
    In this series, c0 is the coefficient of   x–1.
    This value of   r   generates the single term
    y = c0 / x

    At   r = –3 , the series becomes
    c0 & c2 arbitrary; all other cn = 0
    In this series, c0 is the coefficient of   x–3   and   c2 is the coefficient of   x–1.
    This value of   r   generates the two terms
    y = c0 / x^3 + c2 / x
    where c0 and c2 are both arbitrary constants.
    Putting the two results together, the general solution of the ODE is

    y = A / x^3 + B / x

    Additional Note:

    This ODE is an example of a Cauchy-Euler ODE.
    The general form of a Cauchy-Euler ODE is
                      x^2 y" + p x y' + q y = r(x)
    It can be solved by assuming a complementary function of the form
                      y   =   A xm + B xn
    Substitute   y   =   xm   into the ODE:
    x^2 y" + 5x y' + 3y = 0
    m^2 + 4m + 3 = 0
    m = -1, n = -3
    Therefore the general solution is

    y = A / x + B / x^3

  1. Model the initial value problem
                      y' + 2y = 0.01y^3, y(0)=1
    as a perturbation of the linear initial value problem
                      y' + 2y = 0, y(0)=1
    by finding the general solution of
                      y' + 2y = e y^3, y(0)=1
    as a perturbation series, as far as the term in e 2 and evaluating it at e = 0.01 .

    Assume a perturbation series solution of the form
    y = Sum yn e^n, y0(0) = 1, other yn(0) = 0
    Substitute this series into the ODE:
    y' + 2y = e y^3
    This generates the sequence of initial value problems
    y0' + 2 y0 = 0 y0(0) = 1 y1' + 2 y1 = y0^3 y1(0) = 0 y2' + 2 y2 = 3 y0^2 y1 y2(0) = 0
    In all cases, the integrating factor is the same:
    exp(h) = exp(2x)
    For the first initial value problem,
    general solution y0 = C exp(-2x)
    complete solution y0 = exp(-2x)
    For the second initial value problem,
    general solution y1 = exp(-2x) ((-1/4)exp(-4x) + C)
    complete solution y1 = (1/4)[exp(-2x) - (exp(-6x)]
    For the third initial value problem,
    general solution for y2
    complete solution y2 = (3/32)[exp(-2x) - 2(exp(-6x) + exp(-10x)]
    Therefore the perturbation series solution for the initial value problem is

    y = y0 + y1 e + y2 e^2 + ...

    Evaluated at e = 0.01 as far as the term in e 2, the solution is
    y(x; 0.01)
    or

    y = 1.002509 exp(-2x) - 0.002519 exp(-6x) + 0.000001 exp(-10x)

    Additional Note:

    The initial value problem
                      y' + 2y = 0.01y^3, y(0)=1
    is a Bernoulli type of ODE, with   P = 2, R = e   and   n = 3.
    integrating factor = exp(-4x)
    integral (e^h R) dx = -e/4 exp(-4x)
    general solution
    initial condition --> value of C
    complete solution for y^2
    The initial condition is positive, so take the positive square root.
    The exact solution is
                      y = exp(-2x) / sqrt{1 + (1/2)(exp(-4x) - 1)e}

    Find the Maclaurin series expansion of this exact solution (using the binomial expansion):
    Maclaurin / binomial series
    Maclaurin / binomial series
    which is identical to the first three terms of the perturbation series.

  1. BONUS QUESTION:

    A rocket has a mass, when completely empty of fuel and payload, of   r.
    It carries a payload of mass   p.   Initially, it has a mass   f   of fuel aboard.
    Propulsion is provided purely by the expulsion of fuel from the rocket, at a constant rate of   a (kg/s) and a speed relative to the rocket of   u.
    [r, p, f, a and u   are all constants, measured in SI units.]

    1. Develop an ordinary differential equation that governs the speed   v(t)   of the rocket as it travels in free space.

      The initial mass of the rocket is   m(0)   =   p + r + f.
      The last of the fuel is used up at time   T   =   f / a.
      During the time   0 < t < T , the total mass of the rocket is   m(t)   =   p + r + f – at.
      Consider the change in momentum in an elementary interval of time Dt:

      fuel adds momentum (a Dt u) to rocket

      Conservation of momentum
      mv = (m + Dm)(v + Dv) + (-Dm)(v-u)
      [expanding brackets]
      Ignoring the second order term,
      m dv/dt = a u
      Therefore the governing ODE is

      dv/dt = a u / (p + r + f - at)

    2. The rocket starts from rest.   Find its terminal speed (when the last of the fuel has been expelled) in terms of the constants   r, p, f, a and u.
      Integrate dv/dt
      Integrate dv/dt
      Integrate dv/dt

      v = ln | (p + r + f) / (p + r) |

      [Note that the terminal speed is independent of the rate   a   at which the fuel is expended.]

      This classic rocket equation can be rearranged to determine the mass   f   of fuel needed to boost the speed of a rocket of empty mass   mo   by a speed   v:
                        f = mo [exp(v/u) - 1]

    Return to the index of assignment solutions [Return to the index of assignment solutions]
    Return to your previous page [Return to your previous page]