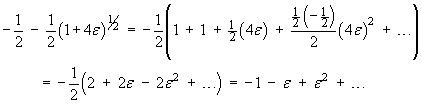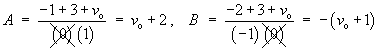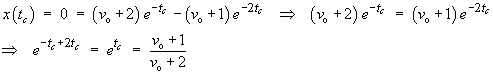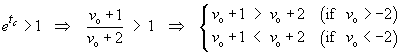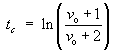BONUS QUESTION:
An over-damped mass-spring system is modelled by the ordinary
differential equation
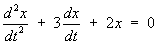
where x(t) is the displacement
of the centre of mass of the spring from its equilibrium
position at time t.
The spring is released with velocity
vo
from location x = +1 at time
t = 0.
Find the condition on the initial velocity
vo in order for the centre
of mass of the spring to pass through its equilibrium
position at some finite positive time
tc and determine an exact
expression for tc in terms
of vo.
Solving the homogeneous ODE:
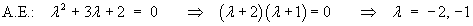
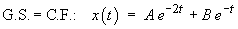
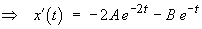
The initial conditions are
x(0) = 1, x'(0) = vo
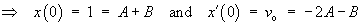
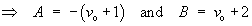
The complete solution is therefore
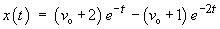
OR using Laplace transforms,
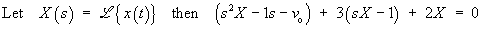
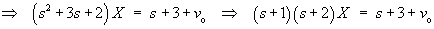
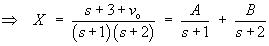
Using the cover-up rule,
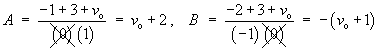
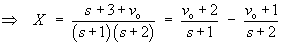
The complete solution is therefore
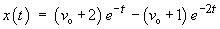
The centre of mass passes through the equilibrium position
x = 0 at time
tc
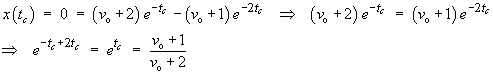
In order for tc to be a positive
real number, we must have
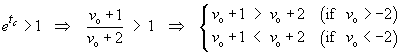
The upper branch has no solution, while the lower branch is
true for all
vo < –2.
Therefore the centre of mass of the spring will pass through
its equilibrium position at the finite positive time
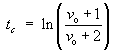
if and only if
![]()
![]()
![]()
![]()
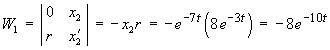
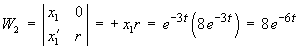
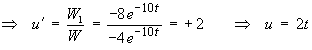
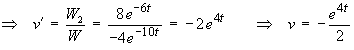
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
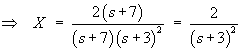
![]()
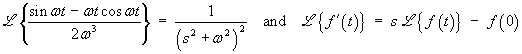
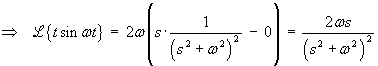
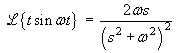

![[values of a3, a4, a5, a6]](m07/q3s.gif)