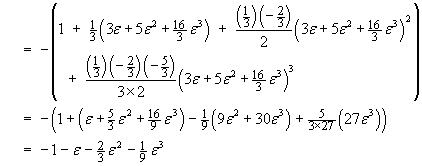![]()
Two methods for a solution are shown here.
Separation of Variables:
![]()
![]()
Pursuing the non-singular solution,
![]()
Imposing the initial condition,
![]()
But the singular solution also satisfies the initial condition!
Therefore the complete solution is
![]()
Conversion to Exact Form (using an integrating factor):
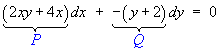
![]()
Try to find an integrating factor as a function of
x only:
![]()
Try to find an integrating factor as a function of
y only:
![]()
![]()
![]()
Multiplying the ODE by I(y) will render
the ODE exact, unless
![]() , when a division by zero occurs.
, when a division by zero occurs.
![]() is a singular solution to the ODE.
is a singular solution to the ODE.
The exact ODE is 2x dx – dy = 0
![]()
Imposing the initial condition,
![]()
But the singular solution also satisfies the initial condition!
Therefore the complete solution is
![]()
![Y(s) = 8 e^(-s) / [s^2 (s^2 + 4)]](m08/q2a.gif)
![Let G(s) = 8 / [s^2 (s^2 + 4)] then
Y(s) = G(s) e^(-s)](m08/q2d.gif)
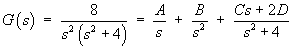
![[Integration property used twice]](m08/q2m.gif)
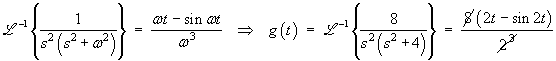
![[shift indices on y"]](m08/q3d.gif)
![a_(n+2) = (1-n) a_n / [(n+2)(n+1)]](m08/q3i.gif)

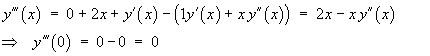
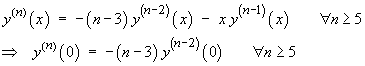
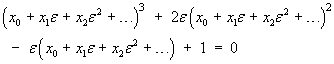
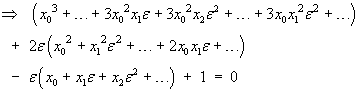
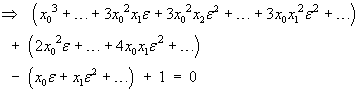
![[table]](m08/q4table.gif)
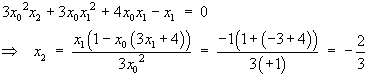
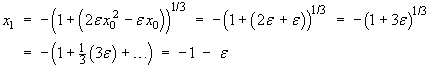
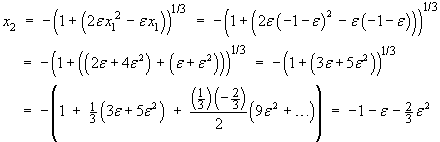
![x3 = -(1 + [3e + 5e^2 + (16/3)e^3])^(1/3)](m08/q4r.gif)