ENGR 1405 Engineering Mathematics 1

Faculty of Engineering and Applied Science
2000 Fall

Problem Set 5
Questions

            In questions 1-6 discuss convergence of the sequence.   

            If it is not given, find the general term.

1.     

         1/7, 5/10, 9/13, 13/16, 17/19, ...

2.     

         0, 3/5, 4/5, 15/17, 12/13, 35/37, 24/25, 63/65, ...

 

3.     

         1/sqrt(14), 1/4, 1/sqrt(18), 1/sqrt(20), ...  

4.     

         [(2)^n + (8)^n]^(1/n)

 

5.     

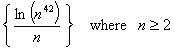
         ln(n^42) / n ; n >= 2

6.     

         sqrt(n+2) - sqrt(n)

 

 

 

 

7.      Every hour each virus that is at least two hours old creates one new copy of itself.

            A newly created copy becomes productive in the same way two hours later.

            Assume that all of these viruses are immortal (never die).

 

            At hour 0 a single virus is created and placed on a petri dish.

            At hour 1 only that single virus is present on the petri dish.

            At hour 2 there are two viruses present (the original and its newly created copy).

 

    (a)   Write down the next seven terms in the sequence { fn } of the number of viruses present at hour n:

                        { 1, 1, 2,    ,    ,    ,    ,    ,    ,    , ... }

[Note:   this sequence is known as the Fibonacci sequence.]

    (b)   Now suppose that each virus becomes productive when only one hour old.   Write down the first four terms and the general term in the sequence { gn } of the number of viruses present at hour n.

    (c)   Is the sequence  { fn }  convergent?

    (d)   Is the sequence  { gn }  convergent?

   In questions 8-10, test the series for convergence.   If it converges, then find its sum.

 

8.     

         Sum(1 to infinity) ((1/3)^n + (1/4)^n)

9.     

         Sum(2 to infinity) (6 / (n^3 - n))

 

10.   

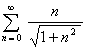
         Sum(0 to infinity) (n / sqrt{1+n^2})

 

 

11.    Write the number 3.142857142857142857...as a ratio of two relatively prime integers.

[Note:  the answer to this question is an ancient approximation to the value of

         p  = 3.14159265... ]

 

 

12.    Every 160 microseconds (= 1.6´10-4 seconds) half of the remaining amount of the C' isotope of the element radium disintegrates radioactively into polonium.   At time t = 0 just over a kilogramme of radium C' is alone in a sealed box.   After 160 microseconds 500 grammes of polonium has been produced.   At  t = 320 microseconds another 250 grammes of polonium has been produced, making 750 grammes in total.   At  t = 480 microseconds another 125 grammes of polonium has been produced, making 875 grammes in total, and so on.

(a)       Find the amount of polonium produced after 160n microseconds, where n is a positive integer.

(b)       Find the total amount of polonium produced in a day, correct to the nearest gramme.

The solutions will appear in another part of this Web site.

Back to the Index of Problem Set Questions  [Back to the Index of Problem Set Questions]

[On to the Index of Solutions]   To the solution page

  [Return to your previous page]

Created 2000 10 11 and modified 2000 10 13 by Dr. G.H. George