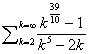ENGR 1405 Engineering Mathematics 1
Faculty of Engineering and
Applied Science
2000 Fall
Problem
Set 6
Questions
In questions 1 and 2 determine all values for k Î ú such that the
given series,
where b > 1, converges.
1.
.
2.
.
Fully discuss the convergence of each of the following series.
In each problem be sure indicate which test is being used and your conclusions.
|
3. |
|
4. |
|
5. |
|
|
|
|
|
|
|
|
|
6. |
|
7. |
|
8. |
|
|
|
|
|
|
|
|
|
9. |
|
10. |
|
11. |
|
|
|
|
|
|
|
|
|
12. |
|
|
|
|
|
13. In a previous Mathematics course it was established that for a, b Î ú with a ¹ 0,
.
(a)
Using the result above write down an expression for 
,
when a < 0.
(b)
Find 
, in simplified form.
(c)
Deduce the value of 
, for the case when a < 0.
14. A ball has a bounce coefficient "r", where 0 < r < 1 is a real number. Each time the ball drops from a height "h" it returns to a height "r ´ h".
(a) Assuming that the ball is allowed to bounce an infinite number of times, determine the general answer for the total distance, D, traveled by the ball.
(b) Find the value of D when the initial height is 9 metres, and r = 0.64.
The solutions will appear in another part of this Web site.
[Return to your
previous page]