Determine whether the series
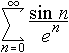 is absolutely convergent, conditionally convergent or divergent.
State which test you are using.
is absolutely convergent, conditionally convergent or divergent.
State which test you are using.
Faculty of Engineering and Applied Science
2000 Fall
[Note: some browsers do not display symbols correctly.
Read
“p” as
“p” (pi),
“Ö” as
“Ö” (square root),
“Þ” as
“Þ” (implies),
“Δ as
“Δ (element of),
“ú” as
“ú” (Real),
“-” as
“-” (minus sign).]
Determine whether the series
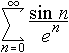 is absolutely convergent, conditionally convergent or divergent.
State which test you are using.
is absolutely convergent, conditionally convergent or divergent.
State which test you are using.
Determine whether the series
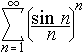 is absolutely convergent, conditionally convergent or divergent.
State which test you are using.
is absolutely convergent, conditionally convergent or divergent.
State which test you are using.
Find the range(s) of values of z for which the
series
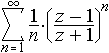 is
is
| (i) | absolutely convergent, |
| (ii) | conditionally convergent, |
| (iii) | divergent. |
For the function f (x) = cos x:
In each of questions 5 to 8, find the Taylor or Maclaurin series for the function and discuss convergence.
Determine the first five (5) non-zero terms of the Maclaurin series expansion for
The solutions will appear in another part of this Web site.
|
|
[On to the Index of Solutions]
|