For the curve defined parametrically by
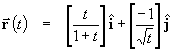 ,
determine
,
determine
- the tangent vector
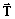 , and
, and - the element of arc length "ds".
Also:
- Eliminate the parameter t to find a Cartesian equation of this curve.
Faculty of Engineering and Applied Science
2000 Fall
Note: if you see symbols like ³ or Þ in various places, then your browser is not reading the style sheet for this Web page properly (or the Symbol font is not installed on your computer). The translation is:
| k = k (kappa) | q = q (theta) |
For the curve defined parametrically by
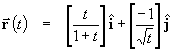 ,
determine
,
determine
Also:
For the curve defined parametrically by
![]() ,
determine
,
determine
For the curve defined parametrically by
![]() ,
determine
,
determine
For the curve whose Cartesian equation is
x2/3 + y2/3 = 1
For the curve of intersection of the plane
![]() and the elliptic cylinder
and the elliptic cylinder
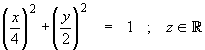 defined parametrically by
defined parametrically by
![]()
find:
For the curve defined parametrically by
![]() ,
determine
,
determine
For the curve defined parametrically by
![]() ,
determine
,
determine
Also:
For the curve defined parametrically by
![]() ,
determine
,
determine
What type of curve is r(p)?.
Determine the unit tangent vector,
![]() ,
the unit principal normal vector,
,
the unit principal normal vector,
![]() ,
and the curvature k
for the curve defined parametrically by
,
and the curvature k
for the curve defined parametrically by
![]() .
.
Also:
Eliminate the parameter t to find a Cartesian equation of this curve.Hence sketch this curve.
Determine the unit tangent vector,
![]() ,
the unit principal normal vector,
,
the unit principal normal vector,
![]() ,
and the curvature k
for the curve defined parametrically by
,
and the curvature k
for the curve defined parametrically by
![]() .
.
The solutions to this problem set are now available.