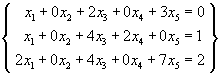MATH 2050 Linear Algebra

(Section 4)
2009 Winter

Assignment 2   -   Questions

[Sections 1.1 - 1.3   Elementary Operations, Gaussian Elimination
and Homogeneous Systems]
Due in class on 2009 January 26 (Monday)

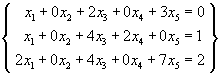  1. x1 + 2x3 + 3x5 = 0 x1 + 4x3 + 2x4 = 1 2x1 + 4x3 + 7x5 = 2         [15 marks]

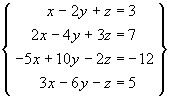  1. x - 2y + z = 3 2x - 4y + 3z = 7 -5x + 10y - 2z = -12 3x - 6y - z = 5         [15 marks]

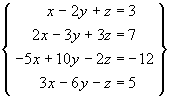  1. x - 2y + z = 3 2x - 3y + 3z = 7 -5x + 10y - 2z = -12 3x - 6y - z = 5         [15 marks]

  1. For the homogeneous linear system
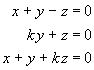
    x + y - z = 0 ky + z = 0 x + y + kz = 0
    find all values of k for which there are non-trivial solutions.         [15 marks]

  1. When any of the three types of row operation is applied to a homogeneous linear system, the resulting linear system is also homogeneous.   Prove that this statement is true.         [10 marks]

  1. Find, where possible, conditions on a and b, such that the system has no solution, one solution or infinitely many solutions.
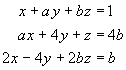                  x + ay + bz = 1 ax + 4y + z = 4b 2x - 4y + 2bz = b         [30 marks]

  Return to the Index of Assignment Questions   [To the Index of Assignments.]   [Solutions to this assignment] To the solutions to this assignment
[Available after January 26]
  Back to previous page   [Return to your previous page]
      Created 2008 12 10 and most recently modified 2008 12 31 by Dr. G.H. George