MATH 2050 Linear Algebra

(Section 4)
2009 Winter

Assignment 5   -   Questions

[Section 3.1   Determinants]
Due in class on 2009 February 16 (Monday)

  1. Find the determinant and the inverse of the matrix         [10 marks]
    A = [ 8 -11 ] [ -2 3 ]

  1. Find the determinant of the matrix         [10 marks]
    R = [ cos theta -sin theta 0 ] [ sin theta cos theta 0 ] [ 0 0 1 ]

  1. Find the determinant of the matrix         [15 marks]
    C = [ 0 1 2 3 ] [ 0 0 2 0 ] [ 3 10 12 20 ] [ 0 0 0 4 ]

  1. Find the determinant of the matrix         [10 marks]
    D = [ 1 3 5 1 1 ] [ 2 1 4 2 2 ] [ 0 4 3 0 3 ] [ -1 -6 2 -1 2 ] [ 2 8 -1 2 1 ]

  1. [Textbook, page 114, exercises 3.1, question 8(b)]                 [20 marks]
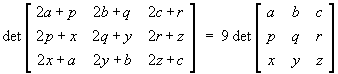
    Show that   | 2a+p 2b+q 2c+r | | a b c | | 2p+x 2q+y 2r+z | = 9 | p q r | | 2x+a 2y+b 2z+c | | x y z |

  1. F = [ 1 1 0 ] [ 2 1 c ] [ c 0 1 ]         [10 marks]
    Find the value(s) of   c   for which the matrix   F   is singular.

  1. If   det X = 2   and   det Y = 3 , then calculate the value of         [15 marks]
    det (X^2 Y^(-1) X^T Y^3)   where possible.
    Under what circumstances does   (X^2 Y^(-1) X^T Y^3)   not exist?.

  1. The general 3×3 skew-symmetric matrix is         [10 marks]
    K = [ 0 a b ] [ -a 0 c ] [ -b -c 0 ]   (where   a, b, c   are any real numbers).
    Find   det K.

  Return to the Index of Assignment Questions   [To the Index of Assignments.]   [Solutions to this assignment] To the solutions to this assignment
[Available after February 16]
  Back to previous page   [Return to your previous page]
      Created 2009 02 02 and most recently modified 2009 02 02 by Dr. G.H. George