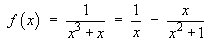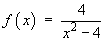
![a / (x+2) + b / (x – 2)]](c5/q1b.gif)
Both denominators are linear non-repeated factors. The cover-up rule may be used:
![[evaluation of a and b]](c5/q1c.gif)
Therefore
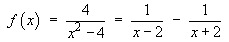
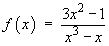
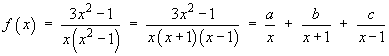
All three denominators are linear non-repeated factors. The cover-up rule may be used:
![[evaluation of a, b and c]](c5/q2c.gif)
Therefore
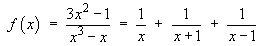
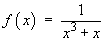
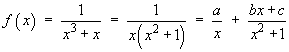
Note that the polynomial in the numerator of a partial fraction must be of order one less than that of the denominator of that partial fraction. Linear denominators need constant numerators, while quadratic denominators require linear numerators.
Only the first denominator is a linear non-repeated factor. The cover-up rule may be used to find a:
![[evaluation of a]](c5/q3c.gif)
One of the standard methods must be used to find b and c.
Clearing the denominators:
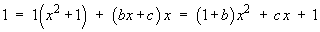 for all x
for all x
Matching coefficients of x2: 0 = 1 + b
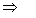 b = – 1
b = – 1Matching coefficients of x1: 0 = c
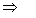 c = 0
c = 0[The coefficients of x0 already match, because we found a = 1 by the cover-up rule.]
Therefore