ENGI 3423 Probability and Statistics

Faculty of Engineering and Applied Science
2010 Fall

Problem Set 1

[Descriptive Statistics]

To be completed by Monday 20 September, 2010.
Compare your solutions with those in the files listed on the solution page.

If, in the set of values
{ 11, 12, 13, 14, 15, 16, 17 } an error causes the value “15” to be replaced by “150”,
1. what effect will this change have on the median value?
2. what effect will this change have on the mean value?
3. what effect will this change have on the mode?
4. which of mean and median is the “better” measure of location for this data set and why?

The total scores obtained on a pair of biased ("loaded") dice when they were thrown 100 times are summarized in the frequency table below:

Score
x Frequency
f Score
x Frequency
f

2 1 8 7

3 0 9 11

4 1 10 20

5 1 11 37

6 2 12 15

7 5 Total: 100

Display this information on a bar chart.
Identify the mode.
Construct the cumulative frequency table and hence find the median.
Find the arithmetic mean.
Find the sample variance.

The grades received by an engineering class in a certain course are as shown in the frequency table below:
```
 
         Grade   Frequency 

           A        34
           B        47
           C        50
           D         8
           F        16 
```
Display this information graphically in the form of
1. a bar chart
2. a pie chart
3. Show the calculation for the angle of any two segments of the pie chart.

In questions 4 to 7 below, use Minitab (or some other software package) to answer the questions.
If you do not use Minitab, then state what software package you have used.

For the following data set, (also available as a plain text file here),

11.0235  11.5425   6.3796  10.6863  11.2498   9.4001   8.1008   9.3688
 7.0824  11.3153   7.6724  11.0376  11.3456  11.4693  11.2637  13.8840
13.4236  12.4395   9.0602  10.3851  12.3451   9.0963   9.9664  10.0884
10.6892  10.2857  11.1531   8.1981   8.8498  10.1541  11.3870   7.8716
10.6421  10.0624   7.9238   9.4103  11.2544   8.3797  11.7105   9.2957

create a printout of Minitab’s standard “Descriptive Statistics Graph” output (as was demonstrated in the Minitab tutorial), (or provide equivalent information from some other software package).
What evidence do you see for skewness in these data?

For the following data set of 100 values, (also available as a plain text file here),

1.86729  3.03009  6.40883  4.33369  0.63779  0.52385  0.45279  3.10719  2.38530  4.67676  
2.27304  2.77329  0.82524  2.85599  1.85314  2.77157  2.85183  0.65357  0.41211  1.91722  
2.47675  1.79431  0.66736  1.53275  3.75922  2.83728  0.72920  1.60064  2.28358  1.67403  
1.03660  0.50900  1.01876  2.59330  0.96129  0.76012  1.16550  0.53473  1.21241  0.67745
3.68679  5.63466  4.42160  0.63746  2.00497  1.42397  1.20251  2.76120  1.32941  2.15488  
2.71581  1.12878  1.08641  1.42361  2.15491  2.36957  3.34404  4.23517  0.86197  1.13020  
0.66336  3.62513  2.76912  2.94111  1.65254  2.56736  0.84466  0.44295  1.48484  4.65815  
5.37489  1.28596  1.67463  0.87603  2.21675  1.52227  0.22268  1.85488  3.86302  0.65238
0.77662  0.29270  2.00163  0.99977  1.60562  1.02060  1.06657  2.29138  0.86205  2.18029  
1.99972  1.29414  2.58438  0.94377  0.33508  1.94735  1.83459  1.88173  1.74026  2.61448

construct a stem-and-leaf diagram, with an interval of 0.5.
create a printout of Minitab’s standard “Descriptive Statistics Graph” output,
(or provide equivalent information from some other software package).
construct a standard boxplot.
identify any outliers (list their values).
construct an histogram, using as class boundaries the consecutive integers, from 0 to the next integer above the largest observed value.
What evidence do you see for skewness in these data?

For the following data set of 30 values, (also available as a plain text file here),
```
    0.957438  0.667277  0.695792  0.513556  0.989805
    0.740677  0.837656  0.811593  0.917656  0.718129
    0.930773  0.921245  0.964071  0.929488  0.901530
    0.985619  0.658793  0.828450  0.971182  0.998991
    0.934772  0.905575  0.856455  0.789214  0.836906
    0.894283  0.529852  0.848346  0.904158  0.961747
```
1. create a printout of Minitab’s standard “Descriptive Statistics Graph” output,
  (or provide equivalent information from some other software package).
2. construct a standard boxplot and add a symbol to indicate the location of the arithmetic mean.
3. identify any outliers (list their values).
4. construct an histogram, using class widths of 0.1, from 0 to 1.
5. What evidence do you see for skewness in these data?

For the following data set of 60 values, (also available as a plain text file here),
```
    72  61  43  54  54  48  48  59  55  61
    50  55  30  66  41  55  48  57  61  48
    46  61  30  50  66  73  54  48  66  61
    45  57  48  70  68  43  52  50  46  64
    46  50  50  50  48  37  45  53  64  50
    39  32  66  68  41  70  48  73  39  43
```
1. construct a frequency bar chart, with classes of width 5 and centres at
  { 32, 37, 42, 47, ... , 67, 72 }.
2. create a printout of Minitab’s standard “Descriptive Statistics” output,
  (or provide equivalent information from some other software package).
3. identify the modal class and the median class from your bar chart.
4. use the grouped data (from the bar chart) to calculate the mean, the population standard deviation and the sample standard deviation (you may find this easier to do in a spreadsheet program such as Microsoft Excel^®).
5. Why are the mean and standard deviation that you calculated in part (d) different from the Minitab values?

Problem Set Bonus Question, Descriptive Statistics

Prove that, for any real constant ,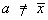
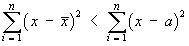
$Sum {(x - xBar)^2} < Sum{(x - a)^2}$

Hint:
Use the identities 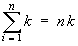(for any constant k ) and .

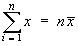Additional Note:
It then follows that, for any random sample of size n drawn from a population of true mean µ,
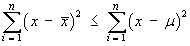$Sum {(x - xBar)^2} <= Sum{(x - mu)^2}$ (with equality only in the very unlikely event that ).
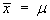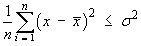
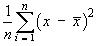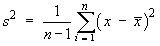One can then speculate [correctly] that, more often than not, $(1/n)*Sum {(x - xBar)^2} <= sigma^2$ $(1/n)*Sum {(x - xBar)^2}$ is said to be a biased estimate of σ², in that it underestimates the true value of σ² on average. The bias disappears when this variance formula is replaced by the sample variance $s^2 = (1/(n-1))*Sum {(x - xBar)^2}$ . We shall see a proof that s² is an unbiased estimate of σ² during the chapter on estimators (Page 9-18 of the Notes).

	[Return to the Index of Problem Sets.]		[Solutions to this problem set]
	[Return to your previous page]

Created 2003 02 16 and most recently modified 2010 07 30 by Dr. G.H. George

Score x	Frequency f	Score x	Frequency f

2	1	8	7
3	0	9	11
4	1	10	20
5	1	11	37
6	2	12	15
7	5	Total:	100