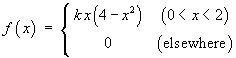
- Find the value of k
- Find the corresponding cumulative distribution function F (x)
- What are the odds that a random quantity having this distribution will take on a value greater than 1?
The probability mass function for X = the number of major defects in a randomly selected appliance of a certain type is
| x | 0 | 1 | 2 | 3 | 4 |
| p(x) | .08 | .15 | .45 | .27 | .05 |
Compute
The discrete random quantity X has the following probability
mass function:
| x | 1 | 2 | 3 | 4 |
| p(x) | .1 | .2 | .3 | .4 |
Now suppose that a random sample of size 100 is drawn from this population.
Find the probability that the sample mean is less than 2.9 .
Find the probability that the sample mean is less than 2.0 .
A small town situated on a main highway has two gas stations, A and B. Station A sells regular, extra, and premium gas for 109.9, 111.1, and 114.4 cents per litre, respectively, while B sells no extra, but sells regular and premium for 108.9 and 114.4 cents per litre, repectively. Of the cars that stop at station A, 50% buy regular, 20% buy extra, and 30% buy premium. Of the cars stopping at B, 60% buy regular and 40% buy premium. Suppose that A gets 60% of the cars that stop for gas in this town, while 40% go to B. Let R = the price per litre paid by the next car that stops for gas in this town.
If a randomly chosen customer has purchased regular gas, then what is the probability that the gas was purchased at station A?
A box of silicon wafers will be withdrawn from a production
line for more intensive testing, if and only if more than one
defective wafer is found in a random sample of 20 wafers, drawn
with replacement from the box.
Let p be the true proportion of defective wafers
in the box.
Let X be the number of defective wafers in the
random sample.
| p | y | |||
|---|---|---|---|---|
| –1 | 0 | 1 | ||
| x | –1 | .10 | .05 | .10 |
| 0 | .15 | .20 | .15 | |
| 1 | .10 | .05 | .10 | |
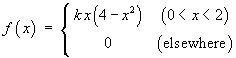
Suppose that the duration (in years) of a construction job can be
modelled as a continuous random quantity t whose cumulative
distribution function (c.d.f.) is given by
Space craft are to be landed at some given point "O" on the moon’s surface, and we wish to observe the position of an actual landing point relative to the aiming point O. Assume that the landing errors are small enough so that it is reasonable to measure them in the tangent plane to the moon’s surface which touches O. Let us further establish a local rectangular coordinate system in that tangent plane which is centered on O and which is oriented so that the x axis points east and the y axis points north.
Suppose that the probability that the space craft lands more than 10 km from the aiming point O is zero and, further, that the probability that the spacecraft lands in some particular region (no point of which is more than 10 km from O) is directly proportional to the area of that region.
Find the probability that the space craft will land
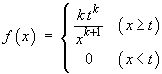
Adam Ant can travel only along the twigs connecting his home
H
with his aunts’ homes
A, B,
C, D,
as shown in the diagram.
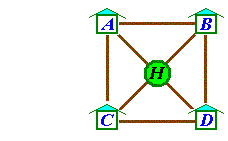
One fine day, Adam decides to visit his aunt at house A.
Then it is time to return home. Being a confused young ant,
his choice of route is random (equal probability for each twig).
Let
A certain atmospheric sensing device has an advertised service life of one year, but it is vulnerable to severe icing. If it survives the full year, then the profit to the owner is 50 (in some units of currency). If an ice storm severe enough to be fatal to the device occurs during its service life, then the profit is reduced by 90 units, unless the owner had invested in protection (costing 15 units), in which case the profit is reduced by 20 units.
An analysis method is available (at a cost of 5 units) which will suggest whether or not such icing will occur during the service life of the device. The analysis is not perfect: in only 95% of all cases where icing fatal to the device occurs, the analysis correctly suggests that such icing will occur. The analysis also suggests fatal icing (incorrectly) in 20% of all cases when no such icing happens.
It is also known from past experience that the probability of icing fatal to the device during the year is 20%.
A box contains 12 good items and 3 defective items
from a factory’s production line. A manager selects four
items at random from the box, without replacement.
Let X = (the number of defective items in the random sample).
Also see the Term Tests from the years 2008, 2007 and 2006.
| [Solutions to these questions]
|
|||