ENGI 4430
Advanced Calculus for Engineering
Course Outline, 2022 Spring
The Memorial University of Newfoundland Code
“All members of the Memorial University of Newfoundland
Community, which includes students, faculty, and staff, shall
treat others with respect and fairness, be responsible and
honest, and uphold the highest standards of academic
integrity.”
The consequences of acts of academic dishonesty can be severe,
as specified in General
Regulation 6.12 of the University Calendar.
Statement of Expectations of Student Conduct
“Like Professional Engineers, engineering students are expected to
behave in a professional manner at all times. Students are
encouraged to conduct themselves in a manner consistent with the
PEG-NL code
of ethics.
MUN has two sets of rules which deal with inappropriate behaviour
by students. The first set deals with
academic
offences
such as cheating while the other set deals with non-academic
offences
such as disruptive behaviour in class. Both sets of rules
can be found in the University Calendar under Regulations.
It is strongly recommended that students read and follow these rules
because the penalties can be severe, the severest being expulsion
from the University.”
Evaluation Scheme
| Best 4 of 5 quizzes (@6.25%): | 25 % |
| One mid term test: | 25 % |
| Final examination | 50 % |
The problem sets
give you some much needed practice in the methods of calculus.
They enhance your chances of success in quizzes, the test and the final
examination, so it is important that you attempt all problem sets
yourself. The questions will be posted on the web site only.
The solutions will be posted on the web site shortly after
the relevant tutorial.
The five quizzes will each be a single question, taking 15 minutes
on alternate Wednesdays (except for Quiz 3), on May 25, June 08,
Fri. June 24, July 06 and July 20.
No deferred quizzes will be offered.
Questions for the mid term test may be drawn from any of the
first six chapters (problem sets 1-5).
The mid term test is scheduled for Wednesday June 15, 12:00 - 13:00.
No deferred tests will be offered.
In the 2022 Spring semester, all quizzes and the term test will be conducted
in person in class.
Marked quizzes and tests will be returned in class.
You will need a calculator for all tests and
examinations. Only simple scientific calculators are permitted
(no capacity for graphics, symbolic algebra, numerical integration,
programming or communication with other devices).
See the calculator policy for
ENGI 4430.
One 8.5" × 11" formula sheet of your
own design (with writing and/or printing on both sides) will be
allowed for the mid term test. Two such sheets will be allowed
in the final examination.
No formula sheets are permitted in any quiz.
Questions in the final examination may be drawn from any part
of the entire course.
Where it is in an individual student’s favour, the weighting
of the final examination for that student may be increased
beyond 50%.
It is the student’s responsibility to locate the time and
place of the final examination.
The Faculty’s examination policies are available from
this
link.
You are reminded of the commitment to uphold the highest
standards of academic integrity.
When you submit any quiz, test or exam,
you unequivocally state that all work is entirely your own and
does not violate Memorial University's Academic Integrity policy.
List of Topics
Parametric and Polar Curve Sketching
Parametric Vector Functions
Arc length (Cartesian and polar); tangent, principal normal
and binormal; curvature; velocity and acceleration (radial,
transverse, tangential and normal components); surface of
revolution (equation, area); area within curves (Cartesian
and polar); review of lines and planes.
Multiple Integration
Double integrals (Cartesian and polar); re-iteration; change
of variables and the Jacobian; second moments; triple integrals
Lines of Force
Numerical Integration
Trapezoidal and Simpson’s rules for numerical
integration; Newton’s method for roots of
f (x) = 0
Gradient, Divergence and Curl
[Cartesian vectors only]
Non-Cartesian Coordinates
Conversion matrices Cartesian to and from polar (cylindrical
and spherical); derivatives of non-Cartesian
basis vectors;
gradient, divergence, curl and Laplacian in any orthonormal
coordinate system
Line Integrals and Green’s Theorem
Work, centre of mass of a wire; path independence; potential
function (in
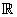 2)
2)
Surface Integration
Projection method; surface method; centre of mass of a
surface; flux
Theorems of Gauss and Stokes
Gauss’ divergence theorem; Archimedes’ principle;
Gauss’ law; Stokes’ theorem; path independence;
potential function (in
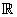 3)
3)
PDEs: d’Alembert solutions
Classification of PDEs; waves on infinite strings;
d’Alembert solutions
PDEs: Fourier solutions
Waves on finite strings; Fourier solutions (separation of
variables)
Textbook
The lecture notes for ENGI 4430 will be available as PDF files
from the Lecture Notes section of this
web site:
“Lecture Notes for ENGI 4430 Advanced Calculus for
Engineering”, by G.H. George (reprint of ninth edition).
You will need to have these notes with you in every class.
A few printed copies may be available at the University Bookstore.
The 2019 edition (or its 2022 reprint) of the lecture notes should be used
in this course.
Anyone using an older edition should read the changes for the 2019-2022 edition.
No one commercial textbook is required for this course.
If you possess textbooks containing the titles
“Advanced Engineering Mathematics”
(such as the textbooks by P.V. O’Neil or D.G. Zill) or
“Multivariable Calculus”,
then you may find
helpful additional examples in those textbooks.
Another option is a cheaper “outline series”
book such as the Schaum’s outline series.
 [Return to your previous page]
[Return to your previous page]
 [Back to the ENGI 4430 Home Page]
[Back to the ENGI 4430 Home Page]
Created 2010 02 22
and most recently modified 2021 11 29
by Dr. G.H. George
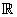 2)
2)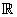 3)
3)