ENGI 5432 Advanced Calculus
Final Examination, 2009 — Questions

Note:   You need the Symbol font (68 kB) in order to display various symbols correctly, such as (otherwise they appear as p, r, q and f ).

1. The function   f (x)   is defined on the interval [0, 1] by

   

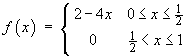
   1. Sketch the even periodic extension of this function.

      [3]

   2. Find the Fourier cosine series for   f (x) .

      [7]

2. The Cartesian equation of a surface   S   is   .

   1. Classify this quadric surface [an answer of less than five words is sufficient].

      [1]

   2. Find the equation of the tangent plane to   S   at the point (1, 2, –2).

      [6]

   3. Hence write down the equations of the normal line to   S   at the point (1, 2, –2) in Cartesian symmetric form.

      [3]

3. A vector field at all points (x, y, z) in is

   

   1. Express this vector field in the cylindrical polar coordinate system.

      [5]

   2. Using the Cartesian coordinate system, find   curl F .

      [3]

   3. Using the cylindrical polar coordinate system, confirm your value for   curl F .

      [4]

4. A vector field is defined on the xy plane by  
   A simple closed path   C   is defined by a triangle whose vertices are at the points (0, 0), (1, 0) and (0, 1).

   1. Can Green’s theorem be used to evaluate the work done by   F   in one circuit of   C ?   Why or why not?

      [4]

   2. Find the exact value of the work done by   F   in one circuit of   C .

      [8]

5. A parabolic cylindrical coordinate system (u, v, w) is related to the Cartesian coordinate system (x, y, z) by the equations

   

   1. Show that the scale factors are  

      [4]

   2. For the vector field evaluate the expression for   div F.

      [4]

   3. For the vector field evaluate the expression for   curl F.

      [4]

   4. On a simply-connected domain that excludes the z-axis, does a potential function exist for F?

      [2]

6. A thin shell   S   is in the shape of part of a cylinder, radius 2 m, centred on the z axis, from z = 0 to z = 1.   The surface density     of the shell at any point (x, y, z) on the shell is    kg m^–2.

   1. What is the range of possible values of the constant   a , if the mass of every part of the shell is non-negative?

      [4]

   2. Find the mass   m   of the shell.

      [5]

   3. Find the location of the centre of mass of the shell.

      [7]

7. Water is flowing along a horizontal cylindrical pipe that has a circular cross section of constant radius a (metre).   The line of symmetry of the cylindrical pipe is aligned along the y-axis.   The velocity of the water at all points in the pipe is

   

   where   v_o   is the maximum speed (in ms^–1) of the water in the pipe.
   Find the rate   Q (in m³s^–1) at which water is flowing across any circular cross section of the pipe.

   [14]

8. For the partial differential equation

   

   1. Classify this partial differential equation (as one of hyperbolic, parabolic or elliptic).

      [2]

   2. Find the general solution   u(x, y).

      [5]

   3. Using the additional information
                   
      find the complete solution   u(x, y).

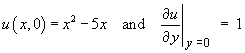
      [5+5]

[Total:   100 marks]

[Back to the Index of Questions]

[On to the Solutions]