ENGI 5432 Advanced Calculus
Final Examination, 2009 — Solutions

  1. The function   f (x)   is defined on the interval [0, 1] by

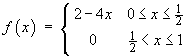
    f(x) = 2-4x (0 < x < 1/2); = 0 (1/2 < x < 1)

    1. Sketch the even periodic extension of this function.

      Even extension of f(x) to [-1, 1]
      Even extension of   f (x)   to [–1, 1]

      Even periodic extension of   f (x)   to the entire real number line [not required by this question]:
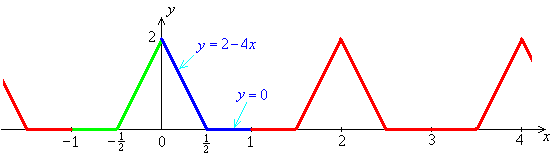
      Periodic extension of f(x) to the entire real number line

      [This latter sketch is of the function to which the Fourier cosine series converges.]

    2. Find the Fourier cosine series for   f (x) .

      L = 1
      Even periodic extension b_n = 0 for all n
      a_0 = [integral]
      a_0 = 1

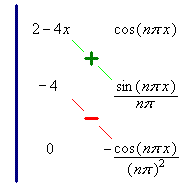
      Tabular integration by parts a_n = [integral]
      a_n = [integral]
      a_n = [integral]
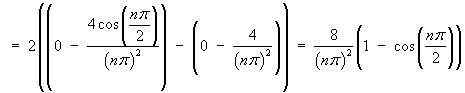
      a_n = 8(1 - cos(n pi/2)) / (n pi)^2
      The Fourier series for any even function is
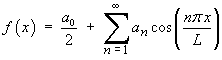
                    a0 / 2 + Sum an cos(n pi x / L)

      Therefore the Fourier cosine series is

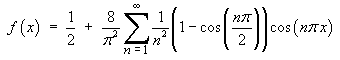
      f(x) = 1/2 + 8/pi^2 Sum{(1 - cos(n pi/2))cos(n pi x) / n^2}

      The first few terms of this series are

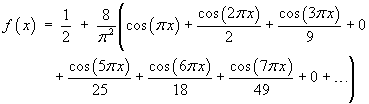
      f(x) = 1/2 + 8/pi^2 {cos(pi x) + cos(2pi x)/2 + cos(3pi x)/9 + 0 + cos(5pi x)/25 + cos(6pi x)/18 + cos(7pi x)/49 + 0 + ...}

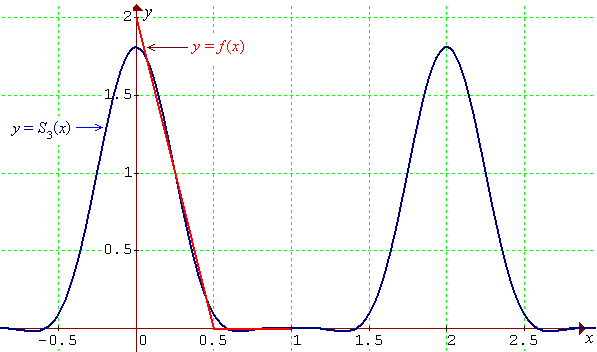
      The graphs of the partial sum of the Fourier series as far as the n = 3 term (in blue) and the original function (in red) are shown here:

      Graphs of S3(x) and f(x)

  1. The Cartesian equation of a surface   S   is   x^2 - y^2 / 4 + z^2 / 4 = 1.

    1. Classify this quadric surface [an answer of less than five words is sufficient].

        hyperboloid of one sheet  

    2. Find the equation of the tangent plane to   S   at the point (1, 2, –2).

      gradient of f = < 2x, -y/2, z/2 >
      normal to plane = < 2, -1, -1 >
      which is a normal vector to the surface at the point (1, 2, –2).
      n dot a = 2
      Therefore the equation of the tangent plane is   n dot r = n dot a

      2x - y - z = 2

    3. Hence write down the equations of the normal line to   S   at the point (1, 2, –2) in Cartesian symmetric form.

      The direction vector of the normal line is the same as the normal vector to the tangent plane.
      The normal line certainly passes through the given point of tangency (1, 2, –2).
      The equations of the normal line, in Cartesian symmetric form, follow immediately:

      (x-1)/2 = (y-2)/(-1) = (z-(-2))/(-1)

  1. A vector field at all points (x, y, z) in real-3 space is

    vector F = [x-y x+y 1]^T

    1. Express this vector field in the cylindrical polar coordinate system.

      Convert the Cartesian components into cylindrical polar form:
      x-y = rho (c-s) , x+y = rho(c+s) , 1 = 1
      Using the coordinate conversion matrix,
      [matrix multiplication]
      ...

      F = rho (rho^ + phi^) + 1 k^

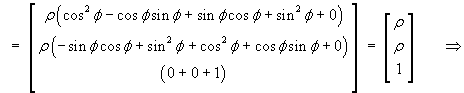
    2. Using the Cartesian coordinate system, find   curl F .

      curl F = [determinant]

      curl F = 2 k^

    3. Using the cylindrical polar coordinate system, confirm your value for   curl F .

      curl F = [determinant]

      curl F = 2 k^

  1. A vector field is defined on the xy plane by   F = (x+1) i^ x/(2-y)^2 j^
    A simple closed path   C   is defined by a triangle whose vertices are at the points (0, 0), (1, 0) and (0, 1).

    1. Can Green’s theorem be used to evaluate the work done by   F   in one circuit of   C ?   Why or why not?

      [plot of triangle enclosed by path C] The only singularities of   F   occur along the line   y = 2 ,
      which is entirely outside   C .
      F   is differentiable everywhere on and inside   C .   Therefore

        YES  

      Green’s theorem can be used to evaluate the work done by   F   in one circuit of   C .

    2. Find the exact value of the work done by   F   in one circuit of   C .

      Using Green’s theorem,
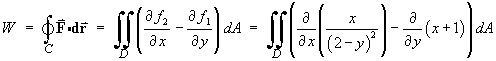
      Line integral = area integral
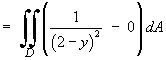
      = integral integral x/(2-y)^2 dA
      [triangular region of integration D] But the region   D   is not a rectangle.
      If the integration with respect to   y   is performed first,
      then the limits on the inner integral run
      from   y = 0   to   y = 1 – x :
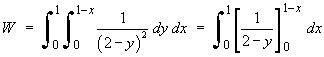
      W = integral integral x/(2-y)^2 dy dx
      [evaluating inner integral]
      [evaluating outer integral]

      If the integration with respect to   x   is performed first, then the limits on the inner integral run from   x = 0   to   x = 1 – y   and the integration is less straightforward:
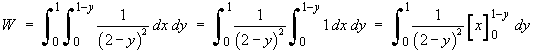
      W = integral integral x/(2-y)^2 dx dy
      [evaluating inner integral]
      [evaluating outer integral]

      The work done may also be calculated using a direct evaluation of the line integral, but this involves three separate integrations and considerably more effort.   By any one of these three methods, the work done is

      work done = ln 2 - 1/2

  1. A parabolic cylindrical coordinate system (u, v, w) is related to the Cartesian coordinate system (x, y, z) by the equations

    x = uv , y = (v^2 - u^2)/2 , z = w

    1. Show that the scale factors are   hu = hv = sqrt(u^2 + v^2) , hw = 1

      vector dr/du = [v -u 0]T --> hu
      vector dr/dv = [u v 0]T --> hv
      vector dr/dw = [0 0 1]T --> hw

    2. For the vector field F = u u^ + v v^ + w w^ evaluate the expression for   div F.

      For any orthonormal coordinate system, the expression for the divergence is
      div F = ...
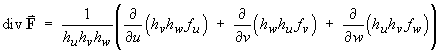
      Using the scale factors from part (a) and the components of   F :
      div F = ...
      div F = ...
      div F = ...
      div F = ...

      div F = 1 + 3/sqrt{u^2 + v^2}

    3. For the vector field F = u u^ + v v^ + w w^ evaluate the expression for   curl F.

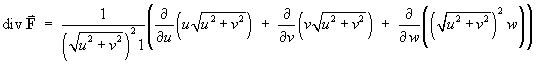
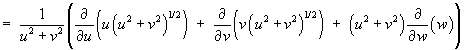
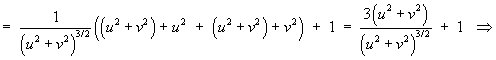
      For any orthonormal coordinate system, the expression for the curl is
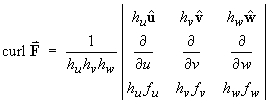
      curl F = ...
      Using the scale factors from part (a) and the components of   F :
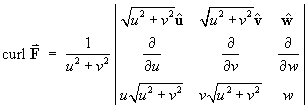
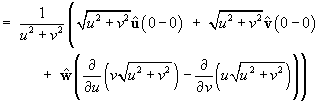
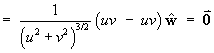
      curl F = ...
      curl F = ...
      curl F = ...
      curl F = ...

      curl F = vector 0

      [with the possible exception of the line   u = v = 0 , which is the z-axis.]

    4. On a simply-connected domain that excludes the z-axis, does a potential function exist for F?

      From part (c) above, curl F = vector 0 everywhere except possibly on the z-axis.   Therefore

        YES  

      on a simply-connected domain that excludes the z-axis, a potential function does exist for F.

  1. A thin shell   S   is in the shape of part of a cylinder, radius 2 m, centred on the z axis, from z = 0 to z = 1.   The surface density   sigma   of the shell at any point (x, y, z) on the shell is   sigma = ax + 2 kg m–2.

    1. What is the range of possible values of the constant   a , if the mass of every part of the shell is non-negative?

      [diagram of cylinder] Non-negative mass requires non-negative density
      But, everywhere on the cylinder,   | x | < 2
      sigma > 0
      The two extreme values of density on the cylinder occur at   x = ±2
      ±2a + 2 > 0
      a > -1 and a < +1
      Therefore the bounds on the parameter   a   are

      -1 < a < +1

    2. Find the mass   m   of the shell.

      The obvious parametric grid to use on this surface is the (phi, z) pair from the cylindrical polar coordinate system.
      The radius of the cylinder is 2 units.
      Therefore   rho = 2   everywhere on the shell.
      The element of area is therefore   dA = 2 d_phi dz
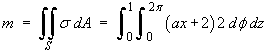
      m = integral (ax+2) 2 d_phi dz
      But everywhere on the cylindrical surface,   x = 2 cos phi :
      m = integral ...
      m = integral ...

      m = 8 pi kg

    3. Find the location (xBar, yBar, zBar) of the centre of mass of the shell.

      The shell has obvious geometric symmetry about the z axis, half way between the bottom and top of the cylinder.
      The surface density depends on   x   only, so that the mass distribution is also symmetric about   y = 0   and   z = ½
      However, the mass distribution is not symmetric about   x = 0 .
      Evaluating the x component only of the moment vector:
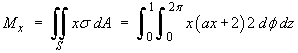
      Mx = integral x(ax+2) 2 d_phi dz
      Mx = integral ...
      Mx = integral ...
      Mx = integral ...
      xBar = Mx / m = a
      Therefore the location of the centre of mass is

      centre of mass at (a, 0, 1/2)

  1. Water is flowing along a horizontal cylindrical pipe that has a circular cross section of constant radius a (metre).   The line of symmetry of the cylindrical pipe is aligned along the y-axis.   The velocity of the water at all points in the pipe is

    v = v0 / a (a - sqrt{x^2 + z^2}) j^

    where   vo   is the maximum speed (in ms–1) of the water in the pipe.
    Find the rate   Q (in m3s–1) at which water is flowing across any circular cross section of the pipe.

    diagram of a section of the pipe 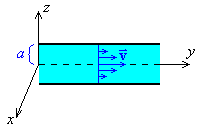All circular cross sections of the pipe are parallel to the xz plane.
    All such cross sections therefore share the same constant normal vector N = j.
    In any cross section   y = constant , use plane polar coordinates:
    x = r cos theta, z = r sin theta
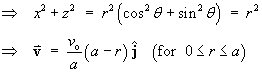
    v = v0 / a (a - r) j^
    Therefore the total flux of water across any circular cross section of the pipe is
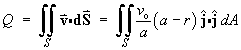
    Q = Integral v dA
    [Evaluating the Integral]
    [Evaluating the Integral]
    [Evaluating the Integral]

    Q = pi a^2 v0 / 3

    One can check that the answer is dimensionally consistent:
    The dimensions of   Q   are (m)2 × (m s–1)   =   (m3s–1)   which is, indeed, the dimensions of volume per unit time.

  1. For the partial differential equation

    2 u_xx + 11 u_xy + 5 u_yy = 4

    1. Classify this partial differential equation (as one of hyperbolic, parabolic or elliptic).

      D = 81 > 0
      Therefore the PDE is everywhere

        hyperbolic  

    2. Find the general solution   u(x, y).

      lambda = -5 or -1/2
      The complementary function is   uc = f(y-5x) + g(y-x/2)
      The right side is a constant (zero-order polynomial) and the left side involves only second partial derivatives.
      Therefore try a second order polynomial as the particular solution:
      uP = ax^2 + bxy + cy^2
      [second derivatives of uP]
      Substituting these partial derivatives into the PDE:
      4a + 11b + 10c = 4
      This is an underdetermined system (only one equation for three unknowns), leaving a free choice for two of the three coefficients.   Choosing   b = c = 0   forces   a = 1   so that   uP = x2 .
      The general solution is the sum of the complementary function and the particular solution:

      u = f(y-5x) + g(y-x/2) + x^2

      Note that other forms of the general solution are valid, such as
      u = f(y-5x) + g(y-x/2) + 0.4 y^2

      Solutions for alternative choices of   a, b, c   are available at this link.

    3. Using the additional information
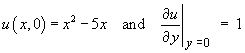
                    u(x,0) = x^2 - 5x , u_y(x,0) = 1
      find the complete solution   u(x, y).

      Starting with the form of the general solution found in part (b) above,
      du/dy
      f'(-5x) + g'(-x/2) = 1 Equation 1
      u(x,0) = f(-5x) + g(-x/2) = -5x Equation 2
      -5 f'(-5x) - g'(-x/2)/2 = -5 Equation 3
      g'(-x/2) = 0
      g(x) = 0
      Note that we can ignore the arbitrary constant of integration here.
      It will cancel out when the complete solution is assembled.
      Equation 2 ==> f(x) = x
      The complete solution is therefore
      u(x,y) = (y-5x) + 0 + x^2

      u(x,y) = x^2 + y - 5x

      It is straightforward to check that this function satisfies both additional conditions and the partial differential equation.

      There are many alternative routes to this solution, but the route shown here is the fastest.