ENGI 5432 Advanced Calculus
Faculty of Engineering and Applied Science2009 Winter
Problem Set 1 - Questions
[Section 1.1 Review of Vectors]Let
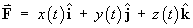 be the position vector of a particle at time t
as it moves along a curve C, where the functions
x(t), y(t) and z(t)
are all differentiable for all values of t.
Show that if
be the position vector of a particle at time t
as it moves along a curve C, where the functions
x(t), y(t) and z(t)
are all differentiable for all values of t.
Show that if 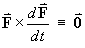 then the particle must always move in the same direction.
then the particle must always move in the same direction.
Let
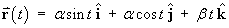 be the position vector of a particle. You may assume that
be the position vector of a particle. You may assume that
 and
and
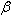 are positive constants.
are positive constants.
- Does the curve lie in one plane?
- What type of curve is it?
There are three formulæ connecting arc length and the unit tangent, unit principal normal and unit binormal vectors, known as the Frenet-Serret formulæ.
Show that the first Frenet-Serret formula is
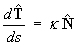 ,
,
where s is arc length and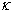 is the curvature.
is the curvature.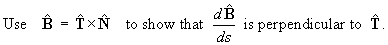
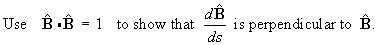
Hence prove the second Frenet-Serret formula
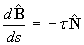 , where the torsion,
, where the torsion,
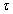 , is some scalar function of
s.
[The torsion is a measure of how much the curve is
twisting out of the plane of
, is some scalar function of
s.
[The torsion is a measure of how much the curve is
twisting out of the plane of
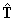 and
and
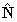 .]
.]Use the fact that
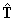 ,
,
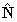 ,
,
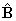 form a mutually orthogonal right-handed triad of unit
vectors, (from which it necessarily follows that
form a mutually orthogonal right-handed triad of unit
vectors, (from which it necessarily follows that
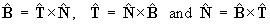 ), to establish the third
Frenet-Serret formula
), to establish the third
Frenet-Serret formula
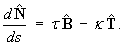
| [Solutions to this problem set]
|
|||