Problem Set 2   -   Questions

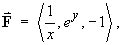
1. find the equations of the lines of force and
2. find the equations of the particular line of force passing through the point   (2, 0, 4).

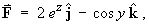
1. find the equations of the lines of force and
2. find the equations of the particular line of force passing through the point   (3, p, 0).

Find the family of vector fields in 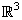whose lines of force are straight lines.

The plane P   passes through the point (2, -1, 5) and contains the line L : y = -3 ,   z = x - 2 .

1. Find the Cartesian equation of the plane P.
2. Find the Cartesian equations of the normal line to   P   that passes through the origin.

Find the [acute] angle q   (to the nearest 0.1°) between the line
       
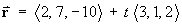
and the plane
       

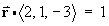
A temperature distribution for a region within 75 metres of the origin is given by
           

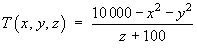
1. Find the gradient of the temperature function   T.
2. Find the [instantaneous] rate at which the temperature is changing at the point (50, 50, 0) in the same direction as the vector i - j .
3. Is the field formed by the gradient vector purely radial?
   [That is, does the gradient vector point directly towards or directly away from the origin at every point?]

Find the equations of the tangent plane and the normal line to the sphere
        x² + y² + z² = 9
at the point (-2, 1, 2).