Problem Set 3   -   Questions

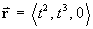
1. Show that the unit tangent is well-defined everywhere along the curve except at the origin.
2. Eliminate the parameter t to find the Cartesian equations of the curve.
3. Sketch the curve.   Display on your sketch the unit tangent 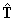and the unit principal normal 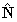at two points close to the origin, one in the region where t < 0 and the other in the region where t > 0 .
4. From your sketch, state briefly why the unit tangent is not defined at the origin.
5. From your sketch, show that the unit binormal 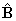has a well defined limit at the origin, (even though the unit tangent and unit principal normal do not).

For the surface whose equation in cartesian coordinates is z² = x² - y²,

1. what type of quadric surface is this surface?
2. find the cartesian equation of the tangent plane to the surface at the point (1, 1, 0).
3. find the cartesian equations of the normal line to the surface at the point (1, 1, 0).

For the surfaces whose cartesian equations are   z = 3x² + 2y²   and   -2x + 7y² - z = 0 :

1. what types of quadric surface are these surfaces?
   
2. find the angle between the surfaces at the point (1, 1, 5).

Calculate the directional derivative of 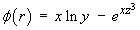at the point (5, 1, -2) in the direction of the vector .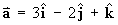

Given that the velocity of a particle at any time   t   is 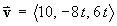and that the particle is at the origin when   t = 0 , find the unit binormal vector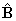 to the curve along which the particle moves and hence find the equation of the plane in which the trajectory of the particle lies.