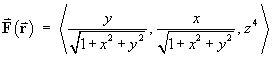Problem Set 4   -   Questions

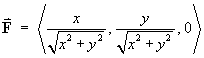
1. Convert   F   from Cartesian coordinates to spherical polar coordinates.

2. Relative to the coordinate axes, in what direction is   F   pointing?

The coordinate conversion matrix   A   for Cartesian coordinates to spherical polar coordinates is

so that   F_sph   =   A F_cart   where

Show that the conversion matrix   B   for the inverse conversion from spherical polar back to Cartesian coordinates, such that   F_cart = B F_sph,   is simply

B = A^T       (the transpose of matrix   A).

Convert from spherical polar to Cartesian coordinates the vector field

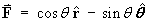
Find the divergence and curl of each of the following:

For the vector field defined in spherical polar coordinates by

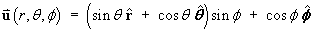
find   .

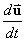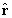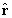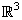Consider the purely radial vector field   F (r, q, f) = f (r) , where is the unit radial vector in the spherical polar coordinate system and   f (r)   is any function of r that is differentiable everywhere in (except possibly at the origin).

1. Find an expression, in terms of   r,   f (r)   and   f ' (r), for the divergence of F.
2. Find an expression, in terms of   r,   f (r)   and   f ' (r), for the curl of F.

3. Of particular interest is the central force law

   

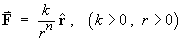
   Show that the divergence of   F   vanishes everywhere in (except possibly at the origin) if and only if   n = 2 .
   [Two of the four fundamental forces of nature, electromagnetism and gravity, both obey this inverse square law.]