ENGI 5432 Advanced Calculus
Faculty of Engineering and Applied Science2009 Winter
Problem Set 5 - Questions
[Sections 1.7, 2.1-2.3]Find the work done when an object is moved along the curve of intersection C of the circular paraboloid
z = x 2 + y 2 and the plane2x + y = 2 from(1, 0, 1) to(0, 2, 4) by a force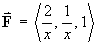 .
.
Find the work done in travelling in
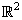 once
anti-clockwise around the unit circle C, centered on
the origin, in the presence of the force
once
anti-clockwise around the unit circle C, centered on
the origin, in the presence of the force
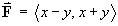 , using both of the
following methods:
, using both of the
following methods:- by direct evaluation of the line integral
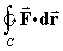 and
and
by using Green’s theorem and evaluating
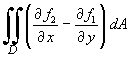 .
.- Is the vector field F conservative?
- by direct evaluation of the line integral
In class we saw that the line integral
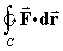 has the value 2p, where
has the value 2p, where
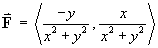 and the path C is one anti-clockwise
circuit of the unit circle centered on the origin.
and the path C is one anti-clockwise
circuit of the unit circle centered on the origin.- Show that the value of the line integral remains
2p when the vector field is replaced
by
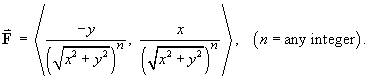
Show that the value of
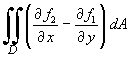 (where D is the circular area
enclosed by C) is not
2p unless
n < 2.
(where D is the circular area
enclosed by C) is not
2p unless
n < 2.Hint: transform the area integral into plane polar coordinates, with
x = r cos q, y = r sin q and dA = dx dy = r dr dq.- Parts (a) and (b) clearly show that Green’s theorem
does not apply when
n > 2.
Why should Green’s theorem not be used whenn > 0 ?
- Show that the value of the line integral remains
2p when the vector field is replaced
by
Find a potential function for the vector field
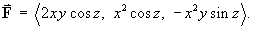
Use this potential function to evaluate the line integral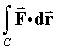 for any piecewise smooth simple curve
C from the point
for any piecewise smooth simple curve
C from the point
(1, 1, -1) to the point(2, 0, 5).
In the evaluation of an area integral
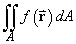 or a volume integral
or a volume integral
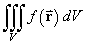 ,
the Cartesian differentials are
related to the differentials of a different parameterization
,
the Cartesian differentials are
related to the differentials of a different parameterization
(u, v, w) of the surface or volume by the Jacobian determinant: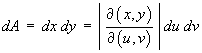
and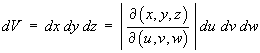 ,
,
where the Jacobian is
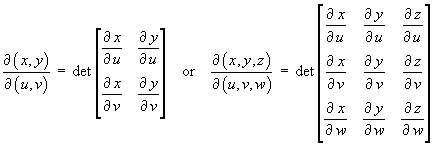 .
.
Evaluate the Jacobian in order to determine the conversion formula from Cartesian differentials dx dy (or dx dy dz) to
- Plane polar area differentials dr dq
- Cylindrical polar volume differentials dr df dz
- Spherical polar volume differentials dr dq df
- Parabolic area differentials du dv, where x = u v, y = v 2 - u 2.
In part (d), sketch on the same x-y plane any three members of each of the two families of coordinate curves u = constant and v = constant.
A thin wire of line density r = (ax + b) e z is laid out along a circle, centre the origin, radius r, in the x-y plane, (where a and b are any real constants and r is any positive real constant).
- Show that a requirement that all parts of the wire have
positive mass leads to the constraint
b > | a | r. - Find the mass of the wire (as a function of a, b and r ).
- Show that the centre of mass is at the point
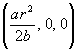 .
.
With the requirement of part (a) in place, what are the maximum and minimum possible distances of the centre of mass from the origin?
The moment of inertia I of a body about an axis of rotation L is defined by
DI = r 2 Dm
(where r is the distance of the element of mass Dm from the axis L).
[The moment of inertia is thus a second moment.]
Find the moment of inertia of the thin wire about the z-axis.The kinetic energy E of a rigid body rotating with angular velocity w about the axis L is given by
E = ½ Iw 2. Find the kinetic energy of the thin wire when it rotates about the z-axis with an angular velocity w.The angular momentum (or moment of momentum) of a rigid body rotating with angular velocity w about the axis L is Iw. [In the absence of any friction or externally applied torque, the angular momentum is conserved.] Find the angular momentum of the thin wire when it rotates about the z-axis with an angular velocity w.
- Show that a requirement that all parts of the wire have
positive mass leads to the constraint
Find the mass and centre of mass of a thin wire that is stretched along a straight line between the origin and the point
(6, 6, 6), given that the line density at(x, y, z) is(x + y + z ) / 100 kg m-1.
| [Solutions to this problem set]
|
|||