ENGI 5432 Advanced Calculus

    Faculty of Engineering and Applied Science
    2009 Winter

    Problem Set 8   -   Questions

    [Sections 1.7, 2.6, 3]

    1. A point charge   Q   at the origin gives rise to the electrostatic potential field

      V = 13/r
      Find

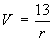
      1. the potential   V   at the point   (x, y, z )   =   (3, -4, 12).
      2. the electric field vector   E   at the point   (x, y, z )   =   (3, -4, 12).
      3. the volume charge density   rV   at the point   (x, y, z )   =   (3, -4, 12).
        [Hint:   use Poisson’s equation   div D = rV .]
      4. the magnitude   Q   of the point charge at the origin.

    1. In spherical polar coordinates, the scalar field V is defined by

      V(x, y, z)   =   r cos2q .

      1. The vector field   F   is defined by F = ÑV .   Find F.
      2. Find the divergence of F.
      3. Find the curl of F.

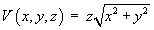
    1. For the scalar field   V(x,y,z) = z * sqrt{x^2 + y^2}

      1. Find   ÑV   in the Cartesian coordinate system.
      2. Find the Laplacian   Ñ2V   in the Cartesian coordinate system in simplified form.
      3. Convert V(x, y, z) to spherical polar coordinates.
      4. Find   ÑV   in the spherical polar coordinate system in simplified form.
      5. Show that the Laplacian   Ñ2V   in the spherical polar coordinate system is cot q.
      6. Hence show that the value of the Laplacian of V is the same in both coordinate systems (except possibly on the z-axis).

    1. A set of functions   {fn(x) }   is said to be orthonormal on the interval   (a, b)   if

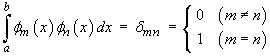
      Integral{phi_m(x)*phi_n(x) dx = 0 (for m not= n) ; = 1 (for m=n)
      where   m   and   n   are positive integers.
      Show that   { sin npx }, { cos npx }   are both orthonormal on the interval (-1, 1).

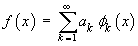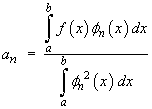      [Note:   It then follows that if f(x) = Sum_k=1 ^oo {a_k phi_k(x)} then a_n = Integral {f(x) phi_n(x)} dx / Integral {(phi_n(x))^2} dx   which leads to methods of series solution of differential equations, including Fourier series.]

    1. Find the Fourier series for the function   f (x)   defined on the interval [–1, 1] by

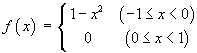
      f(x) = (1 - x^2) on -1 < x < 0; 0 else

    1. Find the Fourier series for the function   f (x)   defined on the interval [–1, 1] by

      f(x) = 1 - |x|

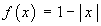
    1. Find the Fourier cosine series for the function   f (x)   defined on the interval [0, 2] by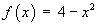

      f(x) = 4 - x^2

    1. Find the Fourier sine series for the function   f (x)   defined on the interval [0, 2] by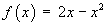

      f(x) = 2x - x^2

      Also comment on why the rate of convergence of this Fourier series everywhere in the interval [0, 2] is much more rapid than in question 7.

    1. [A more challenging question:]
      An incompressible viscous fluid is in steady-state flow around the z-axis, trapped between a pair of coaxial rotating cylinders, aligned along the z-axis.   The inner cylinder has radius a and rotates at angular velocity w k.   The outer cylinder has radius b (> a) and rotates at angular velocity u k.
      In response, the velocity vector at any point in the fluid, in cylindrical polar coordinates (r, f, z), is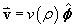   vector v = v(rho) phiHat   and   v(r)   obeys the ordinary differential equation
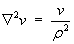
                    Laplacian of v = v / rho^2
      Where it is in contact with a cylinder, the fluid must move with the same velocity as that cylinder.
      Solve the ODE to find the velocity at all points in the fluid.

      Return to the Index of Problem Sets   [To the Index of Problem Sets.]   [Solutions to this problem set] To the solutions to this problem set
      Back to previous page   [Return to your previous page]
    Created 2008 01 01 and most recently modified 2008 12 27 by Dr. G.H. George