ENGI 5432 Advanced Calculus

    Faculty of Engineering and Applied Science
    2009 Winter

    Problem Set 9   -   Questions

    [Sections 4.1-4.5]
    1. Is the function   f (x, y ) = 3 x2y - y3   harmonic and, if so, on what domain?
    1. Find the subsequent motion of an infinite string that is released from rest with the initial displacement
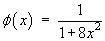
                phi(x) = 1 / (1+8x^2)
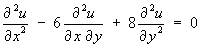
    1. Classify the partial differential equation   u_xx - 6 u_xy + 8 u_yy = 0
      and find its complete solution, given the additional information
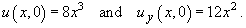
      u(x,0) = 8x^3 , u_y(x,0) = 12x^2
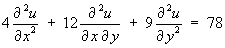
    1. Classify the partial differential equation   4 u_xx + 12 u_xy + 9 u_yy = 78
      and find its complete solution, given the additional information
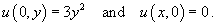
      u(0,y) = 3y^2, u(x,0) = 0
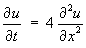    1. Classify the partial differential equation   u_t = 4 u_xx   and find its complete solution on the interval 0 < x < 100 for all positive time t, given the additional information
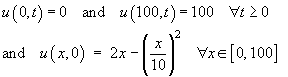
      u(0,t) = 0, u(100,t) = 100, u(x,0) = 2x - (x/10)^2
      Also write down the steady state solution.
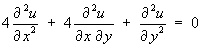    1. Classify the partial differential equation   4 u_xx + 12 u_xy + 9 u_yy = 0   and find its general solution.
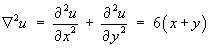    1. Classify the partial differential equation   Laplacian u = u_xx + u_yy = 6(x+y)   and find its general solution.

      Return to the Index of Problem Sets   [To the Index of Problem Sets.]   [Solutions to this problem set] To the solutions to this problem set
      Back to previous page   [Return to your previous page]
    Created 2008 01 01 and most recently modified 2008 12 27 by Dr. G.H. George