ENGI 5432 Advanced Calculus

    Faculty of Engineering and Applied Science
    2009 Winter

    Examples for Potential Functions

      In each case, find the potential function for the vector field,
      (or prove that no such potential function exists).

    1. F = < y+z+yz, x(1+z), x(1+y) >

    1. F = < e^y, x e^y + z^2, 2yz >

    1. F = < -y, x, z >

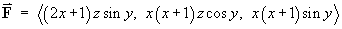
    1. F = < (2x+1)z sin y, x(x+1)z cos y, x(x+1) sin y >
      and the potential is zero on all coordinate planes.

      Return to the Index of Problem Sets   [To the Index of Problem Sets.]   [To the solutions of these examples] To the solutions of these examples
      Back to previous page   [Return to your previous page]
    Created 2008 02 25 and most recently modified 2008 12 27 by Dr. G.H. George