ENGI 5432 Advanced Calculus

    Faculty of Engineering and Applied Science
    2009 Winter

    Term Test 1   -   Questions

    [Chapter 1 and Section 2.1]

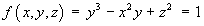    1. For the surface defined by   f = y^3 - x^2 y + z^2 = 1,

      1. Find the equations of the tangent plane and the normal line to the surface at the point (–1, 1, 1).

        [8]

      2. Find, to the nearest degree, the angle that the surface makes with the plane   x + z = 0   at the point (–1, 1, 1).

        [6]

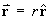    1. The location of a particle is defined in spherical polar coordinates by vector r = scalar r . unit vector r^.
      At any instant,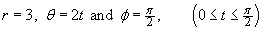   r = 3, theta = 2t, phi = pi/2.
      Find the velocity   v   in spherical polar coordinates.

      [7]

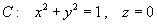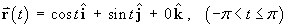    1. A thin wire is in the shape of the unit circle in the xy-plane, C: x^2 + y^2 = 1 , z = 0, which can be parameterized by . r = < cos t, sin t, 0 > , (-pi < t <= pi).
      The line density of the wire is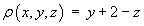   rho = y + 2 - z.

      1. Find the mass and the Cartesian coordinates of the centre of mass of the wire.

        [9]

      2. Find the work done by a force 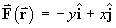F = < -y, x, 0 > in travelling once around the wire.

        [5]

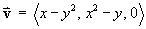
    1. For the velocity field   v = < x - y^2, x^2 - y, 0 >

      1. Find the divergence   div v.

        [5]

        BONUS QUESTION

      1. Find the stream function 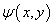psi(x, y) and the family of streamlines for   v.

        [+4]

      2. Find the equation of the streamline that passes through the point (2, 0, 0).

        [+1]

      Return to the Index of Problem Sets   [To the Index of Problem Sets.]   [To the solutions to this test] To the solutions to this test
      Back to previous page   [Return to your previous page]
    Created 2009 01 31 and most recently modified 2009 01 31 by Dr. G.H. George