ENGI 5432/5435 Advanced Calculus

    Faculty of Engineering and Applied Science
    2008 Winter

    Term Test 2   -   Questions

    [Chapter 2]

    1. For the vector function 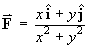  F = (x i^ + y j^) / (x^2 + y^2)   in the x-y plane:

      1. By establishing that there are no singularities of   vector F   in the simply connected domain
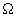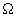        capital Omega   =   { all (x, y) closer than 2 units to the point (2, 2) }, show that Green’s theorem is valid on capital Omega.

        [6]

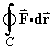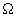      2. Hence evaluate   line integral F.dr, where   C   is one complete circuit around the circle in the x-y plane, centre (2, 2), radius 1, (which is entirely inside the domain capital Omega).

        [14]

    1. For the vector field   F = < y^2 z^3, 2xyz^3 + e^y, 3xy^2 z^2 >:

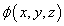      1. By evaluating  curl vector F , show that a potential function   phi(x,y,z)   exists on all of set of real numbers3.

        [8]

      2. Find the potential function 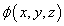  phi(x,y,z)   that is defined in such a way that the potential is zero at the origin.

        [12]

    1. A sheet is in the shape of that part of the circular paraboloid 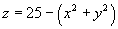  z = 25 - (x^2 + y^2)   that lies between the circular cylinders
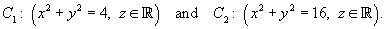
      C1: x^2 + y^2 = 4 and C2: x^2 + y^2 = 16
      The sheet has a surface density of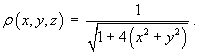

      rho = 1 / sqrt(1 + 4(x^2 + y^2))

      1. Determine the total mass of the sheet.

        [15]

      2. Locate the coordinates 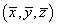  (xBar, yBar, zBar)   of the centre of mass of the sheet.

        [5+5]

      Return to the Index of Problem Sets   [To the Index of Problem Sets.]   [To the solutions to this test] To the solutions to this test
      Back to previous page   [Return to your previous page]
    Created 2008 02 24 and most recently modified 2008 02 24 by Dr. G.H. George