ENGI 5432/5435 Advanced Calculus

    Faculty of Engineering and Applied Science
    2008 Winter

    Term Test 2   -   Solutions

    [Chapter 2]

    1. For the vector function 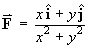  F = (x i^ + y j^) / (x^2 + y^2)   in the x-y plane:

      1. By establishing that there are no singularities of   vector F   in the simply connected domain
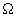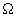        capital Omega   =   { all (x, y) closer than 2 units to the point (2, 2) }, show that Green’s theorem is valid on capital Omega.

        The vector function 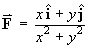  F = (x i^ + y j^) / (x^2 + y^2)   is obviously well-defined (and infinitely differentiable) everywhere except the origin.
        The distance of the origin (0, 0) from the point (2, 2) is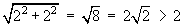 2 sqrt{2} > 2
        The only singularity is outside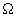   capital Omega.
        Green’s theorem is therefore valid everywhere on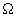 capital Omega.

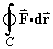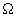      2. Hence evaluate   line integral F.dr, where   C   is one complete circuit around the circle in the x-y plane, centre (2, 2), radius 1, (which is entirely inside the domain capital Omega).

        Green’s theorem [Green's theorem]
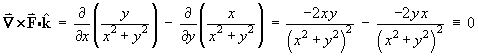
        integrand of surface integral = 0
        everywhere in the domain, including within   C .
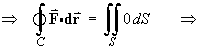
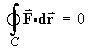
        line integral = 0

        line integral = 0

        [The direct evaluation of the line integral is very difficult and should be avoided!]

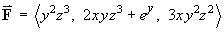    1. For the vector field   F = < y^2 z^3, 2xyz^3 + e^y, 3xy^2 z^2 >:

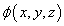      1. By evaluating  curl vector F , show that a potential function   phi(x,y,z)   exists on all of set of real numbers3.

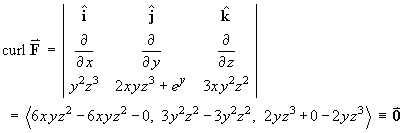
        curl F = zero vector
        Therefore   vector F   is irrotational everywhere and a potential function exists.

      2. Find the potential function 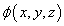  phi(x,y,z)   that is defined in such a way that the potential is zero at the origin.

        The potential function 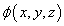  phi(x,y,z)   is such that
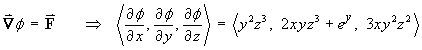
        grad phi = vector F
        [integrate partial dphi/dx]
        where   f (y, z)   is an arbitrary function of integration
        [match partial dphi/dy]
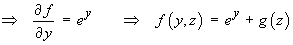
        f(y,z) = e^y + g(z)
        where   g (z)   is another arbitrary function of integration
        [match partial dphi/dz]
        The potential function is therefore
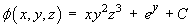
        phi = x y^2 z^3 + e^y + C
        where   C   is an arbitrary constant of integration.
        However, we require that the potential be zero at the origin:
        C = -1
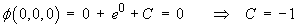
        The potential function is therefore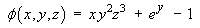

        phi = x y^2 z^3 + e^y - 1

    1. A sheet is in the shape of that part of the circular paraboloid 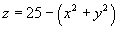  z = 25 - (x^2 + y^2)   that lies between the circular cylinders
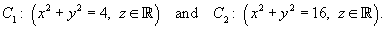
      C1: x^2 + y^2 = 4 and C2: x^2 + y^2 = 16
      The sheet has a surface density of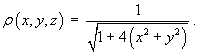

      rho = 1 / sqrt(1 + 4(x^2 + y^2))

      1. Determine the total mass of the sheet.

        Let   r2 = x2 + y2   then the equation of the circular paraboloid becomes   z = 25 - r 2.
        Use the parametric grid (r, q), such that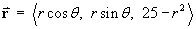   vector r = < r cos t, r sin t, 25 - r^2 >
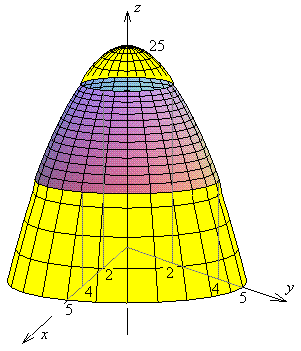
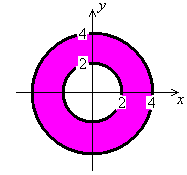
        3D view of paraboloid sheet     shadow of sheet on x-y plane
        The ranges of the parameters are   2 < r < 4   and   0 < q < 2p.
        The tangent vectors along the coordinate grid lines are
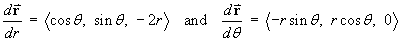
        dr/dr = < cos t, sin t, -2r > and dr/dtheta = < -r sin t, r cos t, 0 >
        A normal vector to the surface at every point is
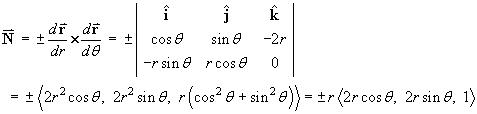
        N = ±r < 2r cos t, 2r sin t, 1 >
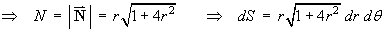
        dS = r sqrt(1 + 4r^2) dr dtheta
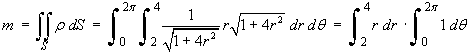
        mass = Integ_2^4 r dr × Integ_0^2pi 1 dtheta
        [evaluating integrals]

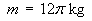
        mass = 12 pi kg

      2. Locate the coordinates 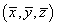  (xBar, yBar, zBar)   of the centre of mass of the sheet.

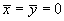
        By symmetry,   xBar = yBar = 0
        Taking moments about the x-y plane,
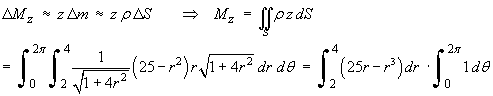
        delta M = z delta m
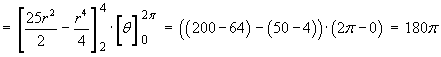
        Mz = 180 pi
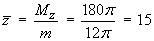
        zBar = Mz / m = 15
        Therefore the centre of mass of the sheet is located at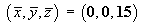

        (0, 0, 15)

        [Note that the centroid is located exactly half way between the bottom and top of the sheet.   As z increases, the decreasing surface area compensates exactly for the increasing surface density.]

      An alternative solution, using the projection method, is available from this link.

          Return to the Index of Solutions   [To the Index of Solutions.]
          Back to previous page   [Return to your previous page]
    Created 2008 02 24 and most recently modified 2008 03 14 by Dr. G.H. George