ENGI 5432 Advanced Calculus

    Faculty of Engineering and Applied Science
    2009 Winter

    Term Test 2   -   Questions

    [Chapter 2]

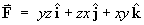    1. For the vector field defined by   F = < yz, zx, xy >,

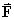
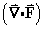
      1. Find the divergence of   vector F   vector F

        [6]

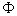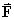      2. Hence find the total flux   scalar capital Phi   of   vector F   through the sphere of radius 1, centre (0, 0, 0).

        [9]

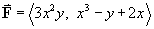    1. In the x-y plane a vector field is defined by F = < 3x^2 y, x^3 - y + 2x >.

      1. Use Green’s theorem to find the work done by 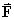  vector F   in one circuit around the unit square (vertices (0, 0), (1, 0), (1, 1) and (0, 1)).

        [17]

      2. Is the vector field 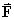  vector F   conservative?   Why or why not?

        [3]

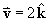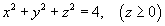    1. The velocity field of a fluid is   v = 2 kHat.   Find the flux   Q   of the fluid through the hemisphere   x^2 + y^2 + z^2 = 4 ; z >= 0   in a direction outward from its centre.

      [25]

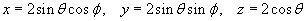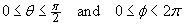
      [Hint:   use a spherical polar coordinate grid   x = 2 sin theta cos phi , y = 2 sin theta sin phi, z = 2 cos theta,   with   0 < theta < pi/2 , 0 < phi < 2 pi

    1.   BONUS QUESTION

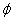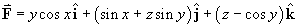      Find the potential function   phi   for   F = < y cos x, (sin x + z sin y), (z - cos y) >   such that 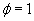  phi = 1   everywhere along the y-axis.

      [+6]

      Return to the Index of Problem Sets   [To the Index of Problem Sets.]   [To the solutions to this test] To the solutions to this test
      Back to previous page   [Return to your previous page]
    Created 2009 03 03 and most recently modified 2009 03 03 by Dr. G.H. George