ENGI 5432/5435 Advanced Calculus

    Faculty of Engineering and Applied Science
    2008 Winter

    Term Test 2 Question 3
    Alternative Solution

    1. A sheet is in the shape of that part of the circular paraboloid 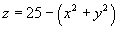  z = 25 - (x^2 + y^2)   that lies between the circular cylinders
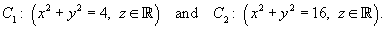
      C1: x^2 + y^2 = 4 and C2: x^2 + y^2 = 16
      The sheet has a surface density of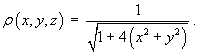

      rho = 1 / sqrt(1 + 4(x^2 + y^2))

      1. Determine the total mass of the sheet.

        Projection Method:

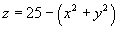
        The equation of the surface is in the explicit form   z = 25 - (x^2 + y^2)
        A normal vector to the surface is
        N = sqrt{1 + 4(x^2 + y^2)}
        mass = Int Int rho N dA = A
        where   A   is the area of the shadow of the sheet on the x-y plane.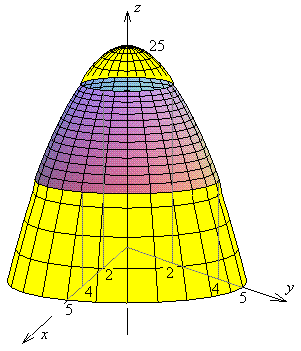

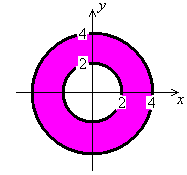
        3D view of paraboloid sheet     shadow of sheet on x-y plane
        The shadow is an annulus, whose area is the difference between the areas of circles of radii 2 and 4:
        A = pi(16-4) = 12 pi

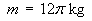
        mass = 12 pi kg

      2. Locate the coordinates 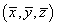  (xBar, yBar, zBar)   of the centre of mass of the sheet.

        Projection Method:

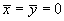
        By symmetry,   xBar = yBar = 0
        Taking moments about the x-y plane,
        delta M = z delta m ==> Mz = Int z dA
        Given the circular geometry of the shadow, use plane polar coordinates in the integral.
        dA = r dr dtheta and z = 25 - r^2
        Mz = Int (25 - r^2)r dr dtheta
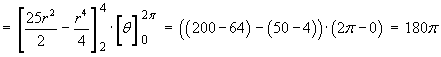
        Mz = 180 pi
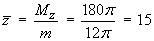
        zBar = Mz / m = 15
        Therefore the centre of mass of the sheet is located at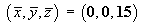

        (0, 0, 15)

        [Note that the centroid is located exactly half way between the bottom and top of the sheet.   As z increases, the decreasing surface area compensates exactly for the increasing surface density.]

          Return to the Solution to Test 2   [Return to the Solution to Test 2.]
          Back to previous page   [Return to your previous page]
    Created 2008 03 25 and most recently modified 2008 03 25 by Dr. G.H. George