ENGI 5432 Advanced Calculus

    Faculty of Engineering and Applied Science
    2009 Winter

    Problem Set 7   -   Solutions

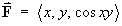    1. Show that no potential function exists for the vector field   F = < x, y, cos xy >.

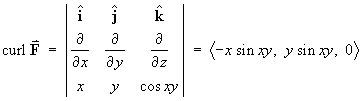
      curl F = < -xsin(xy), ysin(xy), 0 >
      It is not the case that the curl is zero everywhere in   Real Numbers3.
      Therefore no potential function exists for this vector field F

      OR
      Try to find a potential function:
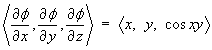
      < dphi/dx, dphi/dy, dphi/dz > = < x, y, cos xy >
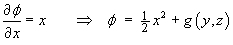
      dphi/dx = x ==> phi = (1/2)x^2 + g(y,z)
      where   g(y, z)   is an arbitrary function of integration.
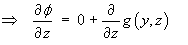      ==> dphi/dx = 0 + (d/dz)g(y,z)   which is not a function of x
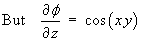      But dphi/dz = cos(xy) which is a function of x
      This is a contradiction.
      Therefore no potential function exists for the vector field F.

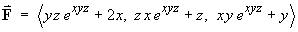
    1. For the vector field   F = < yz exp(xyz) + 2x, zx exp(xyz) + z, xy exp(xyz) + y >
      1. Show that a potential function   V(x, y, z)   does exist.

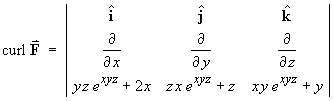
        curl F = | i j k; d/dx d/dy d/dz; yz e^(xyz) + 2x ; zxe^xyz + z ; xye^(xyz) + y
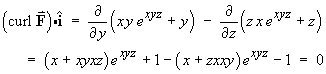
        x-component of (curl F) = 0
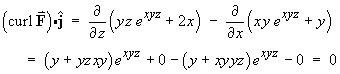
        y-component of (curl F) = 0
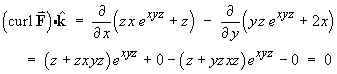
        z-component of (curl F) = 0
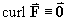        curl F ident= 0 (everywhere in 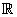Real numbers3), so a potential function V (x, y, z) does exist.
        [or the fact that a potential function can be found in part (b) below
        establishes the answer to this part of the question.]

      2. Find the potential function   V(x, y, z)   that is defined in such a way that the potential is zero at the origin.

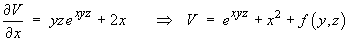
        dV/dx = yz e^(xyz) + 2x ==> V = e^(xyz) + x^2 + f(y,z)
        where   f (y, z)   is an arbitrary function of y and z.
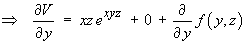
        ==> dV/dy = xz e^(xyz) + 0 + (d/dy)f(y,z)
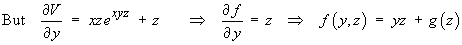
        But dphi/dy = xz e^(xyz) + z ==> df/dy = z ==> f(y,z) = yz + g(z)
        Þ     V   =   exyz + x2 + yz + g (z)
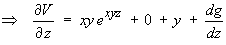
        ==> dV/dz = xy e^(xyz) + 0 + y + dg/dz
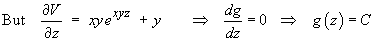
        But dV/dz = xy e^(xyz) + y ==> dg/dz = 0 ==> g(z) = C
        Þ     V   =   exyz + x2 + yz + C
        But   V   =   0   at (0, 0, 0)     Þ     0   =   1 + 0 + 0 + C     Þ     C   =   -1
        Therefore the potential function is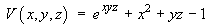

        V = e^(xyz) + x^2 + yz - 1

    1. For the vector field
      F = < x, y, z > / (r exp(r)) , where r = sqrt{x^2 + y^2 + z^2}
      is the distance of the point (x, y, z) from the origin):
      1. Show that a potential function   V(x, y, z)   does exist.

        First note that
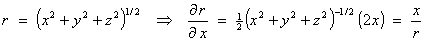
        r = (x^2 + y^2 + z^2)^(t/2) ==> dr/dx = (1/2) (x^2 + y^2 + z^2)^(-1/2) (2x) = x/r
        and, by symmetry,
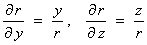
        dr/dy = y/r, dr/dz = z/r
        Thus, for any differentiable function   f(r)
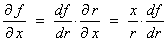        df/dx = df/dr . dr/dx = x/r . df/dr , etc.
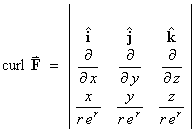
        curl F = | i j k; d/dx d/dy d/dz; x/(re^r) y/(re^r) z/(re^r)
        The x component of   curl F   is
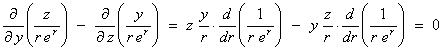
        (d/dy)(z/(re^r)) - (d/dz)(y/(re^r)) = zy/r (d/dr)(1/(re^r)) - yz/r (d/dr)(1/(re^r)) = 0
        and, by symmetry, the other components of   curl F   are also zero.
        curl F ident= 0 (everywhere in Real numbers3), so a potential function V (x, y, z) does exist.

        OR
        F is spherically symmetric.   Switch to spherical polar coordinates
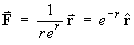
        F = (1/(re')) rHat = (e^(-r)) rHat
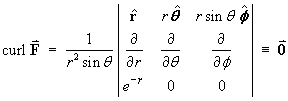
        curl F = (1/((r^2)sin(theta)) | rHat r thetaHat r sin(theta) phiHat ; d/dr d/d(theta) d/d(phi); e^(-r) 0 0 | = 0
        curl F ident= 0 (everywhere in Real numbers3), so a potential function V (x, y, z) does exist.
        [or the fact that a potential function can be found in part (b) below
        establishes the answer to this part of the question.]

      2. Find the potential function   V(x, y, z)   that is defined in such a way that the potential is zero at infinity.   [Hint:   work in spherical polar coordinates.]

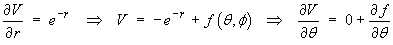
        dV/dr = e^(-r) ==> V = -e^(-r) + f((theta),phi) ==> dV/d(theta) = 0 + df/d(theta)
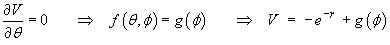
        dV/d(theta) = 0 ==> V = -e^(-r) + g(phi)
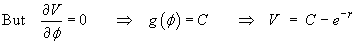
        dV/d(phi) = 0 ==> g(phi) = C ==> V = C - e^(-r)
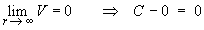
        limit as r --> infinity of V = 0 ==> C = 0
        Therefore the potential function is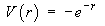

        V(r) = -e^(-r)

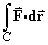
      3. Hence evaluate the line integral   integral_C {F dot dr}
        where   C   is the arc of   { 700x2 + 225z2 = 144,   y = -0.6 }   between the points (0.3, -0.6, 0.6) and (0, -0.6, 0.8).
        [You may leave your answer in terms of powers of   e.]

        The existence of the potential function     Þ     the line integral is path-independent.
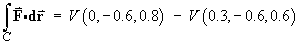
        Integral_C {F dot dr} = V( 0, -0.6, 0.8) - V(0.3, -0.6, -.6)
        At (0, -0.6, 0.8)       r2   =   02 + 0.62 + 0.82   =   1
        At (0.3, -0.6, 0.6)       r2   =   0.32 + 0.62 + 0.62   =   0.92
        Therefore the value of the line integral is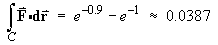

        e^(-0.9) - e^(-1) approx= 0.0387

        In principle the line integral can be evaluated directly, using the parameterization
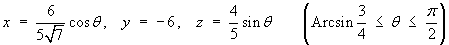
        x= (6/(5(7)^.5))cos(theta), y = -6, z = (4/5)sin(theta), Arcsin (3/4) <= theta <= pi/2
        but the evaluation of the integral is not easy!

      4. Find the absolute maximum and absolute minimum values of the potential function   V.

        V   =   -e -r   has an absolute minimum of   -1   at the origin
        and an absolute maximum of   0   at infinity.

      5. What type of curve is   { 700x2 + 225z2 = 144,   y = -0.6 }?

        It is an ellipse, centre (0, -0.6, 0), in the plane   y = -0.6

    1. Parabolic cylindrical coordinates are defined by
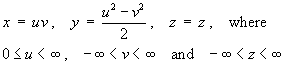
      x = uv , y = (u^2 - v^2) / 2 , z = z , where 0 <= u < oo , -oo < v < oo and -oo < z < oo
      As in question 5(d) of Problem Set 5, the cross-sections of the coordinate “planes” in the x-y plane are parabolas intersecting each other at right angles.   The coordinate surfaces   u = uo   and   v = vo   are therefore vertical parabolic cylinders intersecting each other at right angles, while the third set of coordinate surfaces are the familiar horizontal planes   z = zo.
      1. Determine the scale factors   hu , hv , hz .

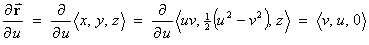
        dr/du = (d/du) < x, y, z > = (d/du) < uv, (u^2 - v^2)/2, z > = < v, u, 0 >
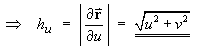
                                                ==> hu = | dr/du | = (u^2 + v^2)^(1/2)
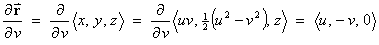
        dr/dv = (2/dv) < x, y, z > = (d/dv) < uv, (u^2 - v^2)/2, z > = < u, -v, 0 >
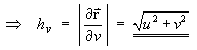
                                                ==> hv = |dr/dv| = (u^2 + v^2)^(1/2)
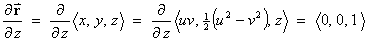
        dr/dz = (2/2Z) < x, y, z > = (d/dz) < uv, .5(u^2 - v^2), z > = < 0, 0, 1 >
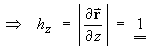
                                                ==> hz = dr/dz = 1

      2. Hence find the expression for the volume element   dV = dx dy dz   in terms of the differentials   du dv dz.
        [The term multiplying   du dv dz   is the Jacobian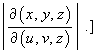 | partiald(x,y,z) / partiald(u,v,z) |

        dV   =   dx dy dz   =   hu hvhzdu dv dz.       Therefore,
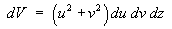
                                                dV = (u^2 + v^2) du dv dz

      3. Determine the gradient vector   Ñf (u, v, z).

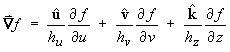
        f = (u^/hu) (df/du) + (v^/hv) (df/dv) + (k^/hz) (df/dz)
        Therefore,
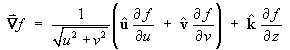
                                                f = 1/(u^2 + v^2)^(1/2) (u^ (df/du) + v^ (df/dv)) + k^ (df/dz)
        (except on the z-axis)

      4. Determine the Laplacian   Ñ2f (u, v, z).

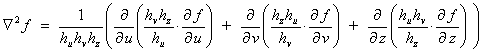
        d = (1/(hu hv hz))( (d/du)((hvhz/hu) (df/du)) + (d/dv)((hzhu/hv) (df/dv)) + (d/dz)((huhv/hz) (dF/dz)))
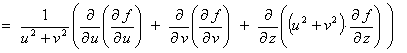
        (1/(u^2 + v^2))( (d/du)(df/du) + (d/dv)(df/dv) + (d/dz)((u^2 + v^2) (df/dz)))
        Therefore,
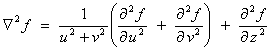
                                                f = (1/(u^2 + v^2)^.5)( (d^2 f/ du^2) + (d^2 f/ dv^2) ) + d^2 f/dz^2
        (except on the z-axis)

    1. Calculate the circulation of 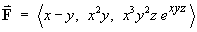  F = < x-y, x^2 y, x^3 y^2 z exp(xyz) >   counterclockwise around the unit circle in the xy-plane.   [Hint:   Use Stokes’ theorem, letting the surface   S   be any smooth surface that has   C   as its boundary.]

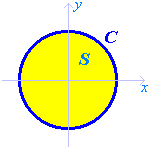      Choose   S   to be the interior of the unit circle C in the x-y plane.

      The domain of   F   is all 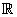Real numbers3, so Stokes’ theorem is valid.
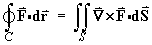
      line integral along C of F = surface integral of curl F
      And on S,   z = 0     Þ
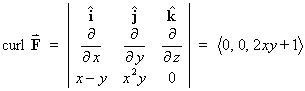
      curl F = | i j k; d/dx d/dy d/dz ; x-y (x^2)y 0 | = < 0, 0, 2xy + 1 >

      Surface net method

      The circular disk suggests the parameters   ( r, q )   such that
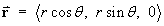
      vector r = < r cos(theta), r sin(theta), 0 >
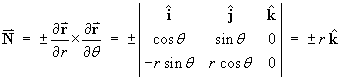
      N = +-(dr/dr) x (dr/d(theta)) = ± | i j k; cos(theta) sin(theta) 0; -r sin(theta) r cos(theta) 0 | = ± rk
      Choose the “outward” normal to be pointing up out of the x-y plane in the direction of increasing z.   Then
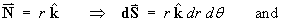
      N = r kHat ==> dS = r kHat dr d(theta)
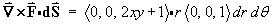
      curl F dot dS = ...
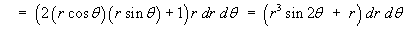
      = (r^3 sin 2(theta) + r) dr d(theta)
      [surface integral of curl F]
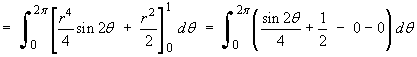
      Integral_0^2pi { (sin (2 theta))/4 + 1/2 - 0 - 0 } d(theta)
      [ -(cos(2 theta))/8 + (theta)/2 ] (evaluated at 2pi, 0) = (-1/8 + pi) - (-1/8 + 0)
      Therefore,
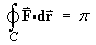
                                              Line Integral_C { F dot dr } = pi

      OR
      Projection method

      In this case, the projection is trivial, as the entire surface is already on the x-y plane.
      Formally,
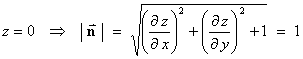
      z=0 ==> |n| = sqrt{(dz/dx)^2 + (dz/dy)^2 + 1} = 1
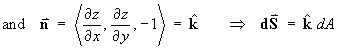
      and vector n = < dz/dx, dz/dy, -1 > = kHat ==> dS = k dA
      But   S   is the interior of a circle, not a rectangle, so use plane polar coordinates.
      dA   =   r dr dq     Þ     dS   =   k r dr dq   and
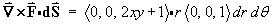
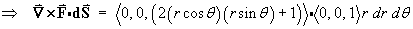
      curl F dot dS = ...
      curl F dot dS = ...
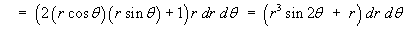
      = (r^3 sin 2(theta) + r) dr d(theta)
      [surface integral of curl F]
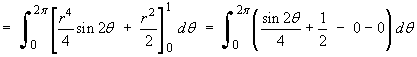
      Integral_0^2pi { (sin (2 theta))/4 + 1/2 - 0 - 0 } d(theta)
      [ -(cos(2 theta))/8 + (theta)/2 ] (evaluated at 2pi, 0) = (-1/8 + pi) - (-1/8 + 0)
      Therefore,
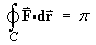
                                              Line Integral_C { F dot dr } = pi

      OR   [ignoring the hint]
      The line integral can be evaluated directly:
      On C an obvious parameterization is
      x = c,   y = s,   z = 0,     where     c = cos q   and   s = sin q
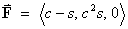
      F = < c-s, c^2 s, 0 >
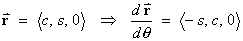
      r = < c, s, 0 > ==> dr/d(theta) = < -s, c, 0 >
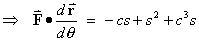
      F dot dr/d(theta) = -cs + s^2 + c^3 s
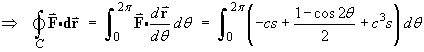
      line integral = ...
      [c^2 / 2 + theta/2 - sin 2theta / 4 - c^4 / 4]_0^2pi
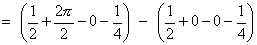
      = (1/2 + pi - 0 - 1/4) - (1/2 + 0 - 0 - 1/4)
      Therefore,
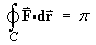
                                              Line Integral_C { F dot dr } = pi

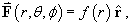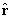    1. Consider the purely radial vector field   F(r,t,f) = f(r) rHat   where   unit vector rHat   is the unit radial vector in the spherical polar coordinate system and   f (r)   is any function of   r   that is differentiable everywhere in real 3-space (except possibly at the origin).
      1. Find an expression, in terms of   r,   f (r)   and   f ' (r), for the divergence of F.

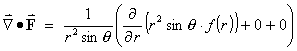
        div F = 1/(r^2 sin theta) (d/dr) (r^2 sin theta f(r))
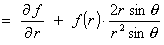
        = df/dr + f(r) 2r sin theta / (r^2 sin theta)
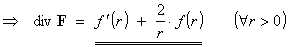
                                                div F = f'(r) + (2/r) f(r)

      2. Find an expression, in terms of   r,   f (r)   and   f ' (r), for the curl of F.

        curl F = [determinant]
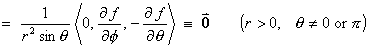
        = 1/(r^2 sin theta) < 0, df/d(phi), -df/d(theta) >
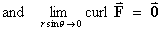
        lim curl F as (r sin theta) --> 0 = vector 0
        Therefore,
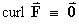
                                                curl F = 0

      3. Is   F   a conservative vector field?

        curl F 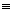ident= 0     Þ     YES,   F is a conservative vector field

      4. Of particular interest is the central force law
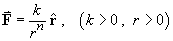
        F = (k/r^n) er (k, r > 0)
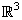        Show that the divergence of   F   vanishes everywhere in real 3-space (except possibly at the origin) if and only if   n = 2 .
        [Two of the four fundamental forces of nature, electromagnetism and gravity, both obey this inverse square law.]

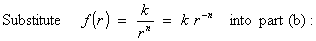
        Substitute f = k/r^n into part (b)
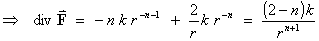
        div F = (2-n)k / r^(n+1)
                                                Þ     div F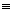 ident= 0   iff   n   =   2.

        [Note:   n = 2   recovers the familiar inverse square law,
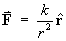
                                                F = (k/r^2) rHat
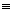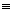                  for which   div F ident= 0   and curl F ident= 0   for all r > 0.]

    1. An extended source of electric charge has a charge density
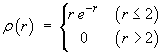
      rho = r exp(-r) , (r <= 2) ; 0 , (r > 2)
      where   r = the distance of the point (x, y, z) from the origin.
      1. Find the total charge   Q   due to this extended object.
        The charge is non-zero on and within a sphere of radius 2, centre the origin.
        Therefore work in spherical polar coordinates.
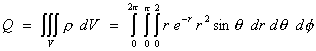
        Q = volume integral of charge density
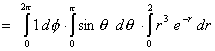
        = product of three single integrals
        = ...
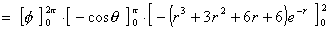
        =   (2p - 0) (1 + 1) (-38e-2 + 6)
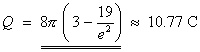
                                                Q = 8 pi (3 - 19/e^2) = 10.77 C

      2. Find the total flux due to the extended charge through the simple closed surface   S   defined by   (x-3)2 + (y-4)2 + z2 = 1.

        S is a sphere, centre (3, 4, 0), radius 1.
        The centre of S is 5 units away from the origin O
        All parts of S are therefore at least 4 units away from O
        The charge extends no more than 2 units away from O.
        Therefore the surface S encloses no charge at all.
                                                [graph of sphere, completely outside the charge]
        From Poisson’s equation   div E ident= 0 everywhere inside S
        Using Gauss’ divergence theorem,
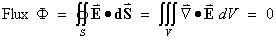
        Flux = surface integral of E = volume integral of div E = 0
        Therefore the total flux through S is zero.

    1. For the vector field   F   =   e- k r r,   where 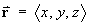vector r = < x, y, z >   and   k   is a positive constant,

      1. find the divergence of   F .

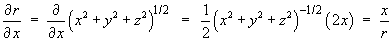
        Note:     dr/dx = d/dx sqrt{x^2 + y^2 + z^2} = (1/2)((x^2 + y^2 + z^2)^(-1/2)) (2x) = x/r
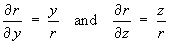
        By symmetry,     dr/dy = y/r and dr/dz = z/r
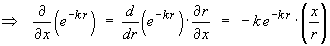
        d/dx(e^(-kr)) = d/dr(e^(-kr)) dr/dx = (-x/r) k e^(-kr)
        and by symmetry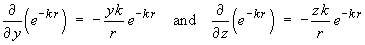     d/dy(e^(-kr)) = (-yk/r) e^(-kr) and d/dz(e^(-kr)) = (-zk/r) e^(-kr)

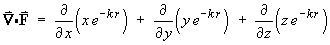
        div F = d/dx(xe^(-kr)) + d/dy(ye^(-kr)) + d/dz(ze^(-kr))
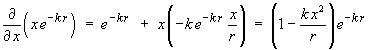
        d/dx(x e^(-kr)) = (1 - (kx^2)/r)e^(-kr)
        and the other two partial derivatives follow by symmetry
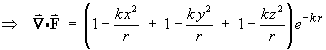
        ==> div F = (1 - (kx^2)/r + 1 - (ky^2)/r + 1 - (kz^2)/r) e^(-kr)
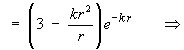
        = ( 3 - (kr^2)/r )e^(-kr)

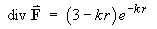
        div F = (3 - kr) e^(-kr)

      2. find the curl of   F .
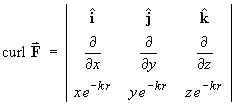
        curl F = | i j k ; d/dx d/dy d/dz ; xe^(-kr) ye^(-kr) ze^(-kr) |
        The x component of   curl F   is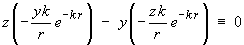   z(-(yk/r) e^(-kr)) - y(-(zk/r) e^(-kr))
        The y component of   curl F   is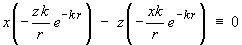   x(-(zk/r) e^(-kr)) - z(-(xk/r) e^(-kr))
        The z component of   curl F   is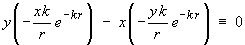   y(-(xk/r) e^(-kr)) - x(-(yk/r) e^(-kr)))
        Therefore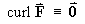

        curl F ident= 0

        and   F   is IRROTATIONAL
        [Note:   All purely radial vector fields are irrotational.]

      3. find where   div F = 0   and classify this surface.

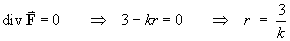
        div F = 0 ==> 3-kr = 0 ==> r = 3/k
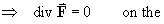
        div F = 0 on the

          sphere, radius 3/k, centre at the origin.  

      4. find where the magnitude   F   of the vector field   F   attains its maximum value.

        F > 0   and is differentiable for all   r > 0
        F (0) = 0   and   F   decreases asymptotically to zero as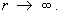   r goes to infinity
        A sole extremum in   r > 0   must therefore be the absolute maximum.
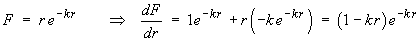
        F = re^(-kr) ==> dF/dr = (1 - rk) e^(-kr)
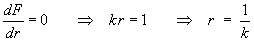
        dF/dr = 0 ==> rk = 1 ==> r = 1/k
        Þ     Fmax   occurs on the

          sphere, radius 1/k, centre at the origin.  

      5. show tha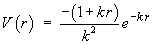t   V(r) = - (1 + kr) / k^2 * exp(-kr)   is a potential function for the vector field   F.

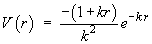
        V(r) = )(-(1+kr))/(k^2))(e^(-kr))
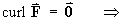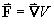
        curl vector F = zero vector a potential function   V   exists such that   vector F = gradient of V
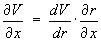        partial dV/dx = dV/dr(V) partial dr/dx     (chain rule)
        = xe^(-kr)
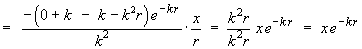
        By symmetry,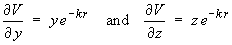     dV/dy = y e^(-kr) , dV/dz = z e^(-kr)
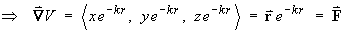
        ==> V = < xe^(-kr), ye^(-kr), ze^(-kr) > = (vector r) e^(-kr) = vector F
        Therefore,   V   is a potential function for F.

      6. find the work done to move a particle from the origin to a place where   div F = 0.

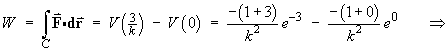
        W = line integral F dr = V(3/k) - V(0)

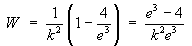
        W = (1/(k^2))(1-4/(e^3)) = (e^3 - 4)/(k^2e^3)

    Return to Index of Problem Set Solutions   [Return to the Index of Solutions.]
    Back to previous page   [Return to your previous page]
    Created 2008 01 16 and most recently modified 2008 12 27 by Dr. G.H. George